- ХАУСДОРФА - ЮНГА НЕРАВЕНСТВА
-оценки коэффициентов Фурье функций из L р;установлены У. Юнгом [1] и Ф. Хаусдорфом [2]. Пусть
-ортонормированная система функций на [ а, b],
для всех 
и всех n = 1, 2, ... и 
Если
то 
где с n (f)- коэффициенты Фурье функции f. Если
то существует такая функция, что g 
В качестве g(t)можно взять
причем этот ряд сходится в Lp'.
X.- Ю. н. (1) и (2) эквивалентны. Для р>2 они не имеют места. Более того, если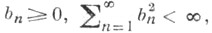
то существует такая непрерывная функция f, что ее коэффициенты Фурье по тригонометрич. системе с n (f) удовлетворяют условию | с n (f)| > bn. Качественная формулировка X.- Ю. н. (если 
то 
для неограниченных ортонормированных систем функций, вообще говоря, не имеет места. Аналог X.- Ю. н. справедлив для широкого класса функциональных пространств. Лит.:[1] Ypung W., лProc. Lond. Math. Soc.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
