- Билинейная интерполяция
-
Билинейная интерполяция — в вычислительной математике расширение линейной интерполяции для функций двух переменных. Ключевая идея заключается в том, чтобы провести обычную линейную интерполяцию сначала в одном направлении, затем в другом.
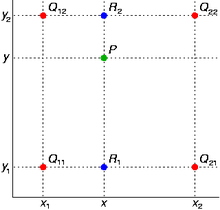
Допустим, что необходимо интерполировать значение функции f в точке P = (x, y). Для этого необходимо знать значения функций в (окружающих P) точках Q11 = (x1, y1), Q12 = (x1, y2), Q21 = (x2, y1), и Q22 = (x2, y2).
Первым шагом интерполируется (линейно) значение вспомогательных точек
 и
и  вдоль оси абсцисс, где
вдоль оси абсцисс, гдеТеперь проводится линейная интерполяция между вспомогательными точками
 и
и  .
.Это и есть приблизительное значение функции в точке P, то есть f(x, y).
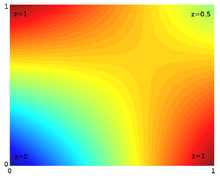
В особом случае, когда известные точки находятся на вершинах единичного квадрата, то есть имеют координаты (0, 0), (0, 1), (1, 0), и (1, 1), формула билинейной интерполяции упрощается до
Или же с помощью умножения векторов с матрицей:
Обратите внимание: сам интерполянт нелинеен:
так как является произведением двух линейных функций. Альтернативное написание:
где



 .
.
Результат билинейной интерполяции не зависит от порядка шагов. Возможно сначала интерполировать между известными точками вдоль оси ординат и затем, получив два вспомогательных значения, интерполировать между ними вдоль оси абсцисс. Результат будет тот же.
Очевидное расширение билинейной интерполяции на функции трех переменных — трилинейная интерполяция.
Содержание
Билинейная интерполяция в компьютерной графике
 Пример увеличения части изображения — простым масштабированием и с применением билинейной интерполяции
Пример увеличения части изображения — простым масштабированием и с применением билинейной интерполяцииВ компьютерной графике билинейная интерполяция получила широкое распространение в процессе ресемплинга (или, проще говоря, масштабирования) изображений.
При увеличении цифровых изображений наблюдается сильная пикселизация картинки. Билинейная интерполяция используется для расчета цветов дополнительных пикселей (
 ) относительно основных, исходных (
) относительно основных, исходных ( ), что позволяет сглаживать переходы. Значением функции
), что позволяет сглаживать переходы. Значением функции  в данном случае выступает цвет пикселя (его составляющие). При этом квадрат, образованный четырьмя рассматриваемыми основными точками принимается единичным.
в данном случае выступает цвет пикселя (его составляющие). При этом квадрат, образованный четырьмя рассматриваемыми основными точками принимается единичным.Недостаток метода
Главным минусом билинейной интерполяции при масштабировании изображений является тот факт, что при увеличении в
 раз изображения размером
раз изображения размером  на
на  пикселей в результате будет получено изображение размером не
пикселей в результате будет получено изображение размером не  на
на  пикселей, а
пикселей, а  на
на  пикселей.
пикселей.Связано это с тем, что в исходном изображении, например, по горизонтали имеется
 точек, то есть
точек, то есть  смежных пар. При увеличении изображения в
смежных пар. При увеличении изображения в  раз между каждой парой основных точек вставляется по
раз между каждой парой основных точек вставляется по  дополнительных точек (то есть при увеличении вдвое между основными точками вставляется еще по одной, при увеличении втрое — по две и т. д.). Итого в результате ширина результирующего изображения будет равна сумме количества основных и дополнительных точек:
дополнительных точек (то есть при увеличении вдвое между основными точками вставляется еще по одной, при увеличении втрое — по две и т. д.). Итого в результате ширина результирующего изображения будет равна сумме количества основных и дополнительных точек: .
.
Проще говоря, для последнего пикселя (в каждой строке и столбце) исходного изображения не находится пары, с которой можно было бы провести интерполирование.
Для обхода данного ограничения, во-первых, обычно принимается, что в исходном и полученном изображениях цветовые значения пикселей сэмплированы из их центров, нежели из углов, т.е. например, если принять абсолютную длину и ширину изображения равными 1, в изображении размером 2 на 2 координатами исходных точек являются (0.25;0.25), (0.25;0.75), (0.75;0.25), и (0.75;0.75), нежели (0;0), (0;0.5), (0.5;0), и (0.5;0.5) (поправка на дискретизацию). Таким образом обеспечивается правильная центровка изображения при масштабировании, но проблемными оказываются не только последняя строка и последний столбец, а все пограничные пиксели получаемого изображения в равной степени, ибо их координаты выпадают за пределы прямоугольника, очерчивающего точки сэмплирования исходного изображения (например, при масштабировании в 4 на 4 нужно вычислить значения в точках (0.125;0.125), (0.125;0.875) и т.д.). Затем, т.к. значения в этих точках не могут быть интерполированы, то нужно расширить исходное изображение одним из способов (выбор которого зависит от способа дальнейшего использования изображения):
- Экстраполяция значений краевых пикселей;
- Зеркальное отражение исходного изображения относительно каждого края, и центральное по углам. В качестве значений отсутствующих пикселей используются копии значений пикселей с того же края; таким образом, пиксели, выпадающие за исходные координаты, являются интерполянтами лишь в одном измерении, а в другом копиями краевых значений;
- Тесселяция исходного изображения; копии исходного изображения "приклеиваются" встык с каждого края и из углов. В качестве цветовых значений отсутствующих пикселей, таким образом, используются значения пикселей с противоположного края. Метод подходит, если интерполированное изображение само будет использоваться для тесселяции (например, для заполнения многоугольников при текстурировании).
После подобной предварительной обработки процедура билинейной интерполяции применяется в исходном виде, с получением изображения ожидаемого размера (
 на
на  ).
).Пример программы
Ниже приведен пример программы билинейной интерполяции изображения, написанный на C
Входные параметры:
a - указатель на массив пикселей изображения, которое необходимо увеличить (уменьшить) Нумерация элементов [0..old_h-1, 0..old_w-1] oldw - старая ширина изображения oldh - старая высота изображенияВыходные параметры:
b - указатель на массив пикселей ресемплированного изображения Нумерация элементов [0..new_h-1, 0..new_w-1] neww - новая ширина изображения newh - новая высота изображения#include <stdio.h> #include <math.h> #include <sys/types.h> void resample(void *a, void *b, int oldw, int oldh, int neww, int newh) { int i; int j; int l; int c; float t; float u; float tmp; float d1, d2, d3, d4; u_int p1, p2, p3, p4; /* Окрестные пикселы */ u_char red, green, blue; for (i = 0; i < newh; i++) { for (j = 0; j < neww; j++) { tmp = (float) (i) / (float) (newh - 1) * (oldh - 1); l = (int) floor(tmp); if (l < 0) { l = 0; } else { if (l >= oldh - 1) { l = oldh - 2; } } u = tmp - l; tmp = (float) (j) / (float) (neww - 1) * (oldw - 1); c = (int) floor(tmp); if (c < 0) { c = 0; } else { if (c >= oldw - 1) { c = oldw - 2; } } t = tmp - c; /* Коэффициенты */ d1 = (1 - t) * (1 - u); d2 = t * (1 - u); d3 = t * u; d4 = (1 - t) * u; /* Окрестные пиксели: a[i][j] */ p1 = *((u_int*)a + (l * oldw) + c); p2 = *((u_int*)a + (l * oldw) + c + 1); p3 = *((u_int*)a + ((l + 1)* oldw) + c + 1); p4 = *((u_int*)a + ((l + 1)* oldw) + c); /* Компоненты */ blue = (u_char)p1 * d1 + (u_char)p2 * d2 + (u_char)p3 * d3 + (u_char)p4 * d4; green = (u_char)(p1 >> 8) * d1 + (u_char)(p2 >> 8) * d2 + (u_char)(p3 >> 8) * d3 + (u_char)(p4 >> 8) * d4; red = (u_char)(p1 >> 16) * d1 + (u_char)(p2 >> 16) * d2 + (u_char)(p3 >> 16) * d3 + (u_char)(p4 >> 16) * d4; /* Новый пиксел из R G B */ *((u_int*)b + (i * neww) + j) = (red << 16) | (green << 8) | (blue); } } }
См. также
Категории:- Вычислительная математика
- Интерполяция
- Геометрические алгоритмы
Wikimedia Foundation. 2010.