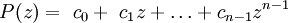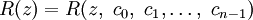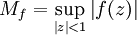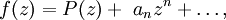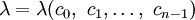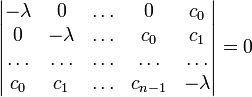- Теорема Каратеодори — Фейера
-
Теорема Каратеодори — Фейера
Теорема Каратеодори — Фейера:
Пусть
многочлен,
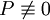 . Существует единственная рациональная функция
. Существует единственная рациональная функциявида
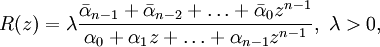
регулярная в
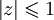 и имеющая в своём разложении в ряд Маклорена n первых коэффициентов, равных соответственно
и имеющая в своём разложении в ряд Маклорена n первых коэффициентов, равных соответственно 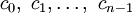 . Эта функция, и только она, реализует наименьшее значение
. Эта функция, и только она, реализует наименьшее значениев классе всех регулярных в круге
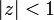 функций f(z) вида
функций f(z) видаи указанное наименьшее значение равно
Число
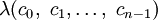 равно наибольшему положительному корню уравнения 2n-й степени
равно наибольшему положительному корню уравнения 2n-й степениЕсли
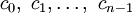 — действительные числа, то
— действительные числа, то 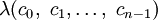 являются наибольшим из абсолютных значений корней уравнения
являются наибольшим из абсолютных значений корней уравнения 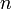 -й степени
-й степениЛитература
- Carathéodory C., Fejer L. Rend. Circolo mat. Palermo, — 1911, v. 32, p. 218—239.
- Голузин Г. М. Геометрическая теория функций комплексного переменного, 2 изд., — М., 1966.
Wikimedia Foundation. 2010.
Теорема Каратеодори — Теорема Каратеодори Фейера: Пусть многочлен, . Существует единственная рациональная функция вида регулярная в … Википедия
Теорема Каратеодори-Фейера — … Википедия
Каратеодори-Фейера теорема — Теорема Каратеодори Фейера: Пусть многочлен, . Существует единственная рациональная функция вида регулярная в … Википедия
Каратеодори-Фейера задача — Теорема Каратеодори Фейера: Пусть многочлен, . Существует единственная рациональная функция вида регулярная в … Википедия
Каратеодори К. — Каратеодори, Константин Дата рождения: 13 сентября, 1873 Научная сфера: математика Константин Каратеодори (Caratheodory) (13 сентября, 1873 года, Берлин 2 февраля, 1950 года, Мюнхен) немецкий математик греческой национальности. Выпускник… … Википедия
Каратеодори Константин — Каратеодори, Константин Дата рождения: 13 сентября, 1873 Научная сфера: математика Константин Каратеодори (Caratheodory) (13 сентября, 1873 года, Берлин 2 февраля, 1950 года, Мюнхен) немецкий математик греческой национальности. Выпускник… … Википедия
Каратеодори, Константин — В Википедии есть статьи о других людях с такой фамилией, см. Каратеодори. Каратеодори, Константин Constantin Carathéodory … Википедия
КАРАТЕОДОРИ - ФЕЙЕРА ЗАДАЧА — задача о продолжимости многочлена от z до степенного ряда, представляющего собой регулярную в круге |z|<1 функцию, реализующую наименьшее значение супремума модуля в круге |z|<1 в классе всех регулярных в |z|<1 функций, к рые имеют… … Математическая энциклопедия
Задача Каратеодори-Фейера — Теорема Каратеодори Фейера: Пусть многочлен, . Существует единственная рациональная функция вида регулярная в … Википедия
Задача Каратеодори — Фейера — Теорема Каратеодори Фейера: Пусть многочлен, . Существует единственная рациональная функция вида регулярная в … Википедия