- Число Армстронга
-
Самовлюблённое число, или совершенный цифровой инвариант (англ. pluperfect digital invariant, PPDI или число Армстронга — натуральное число, которое в данной системе счисления равно сумме своих цифр, возведённых в степень, равную количеству его цифр. Иногда чтобы считать число таковым, достаточно, чтобы степени, в которые возводятся цифры, были равны m — тогда число можно назвать m-самовлюблённым.
Например, десятичное число 153 — число Армстронга, потому что:
- 1³ + 5³ + 3³ = 153
Содержание
Формальное определение
Пусть
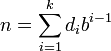 — число, записываемое dkdk − 1...d1 в системе счиления с основанием b.
— число, записываемое dkdk − 1...d1 в системе счиления с основанием b.Если при некотором m случится так, что
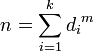 , то n является m-самовлюблённым числом. Если, сверх того, m = k, то n можно назвать истинным числом Армстронга.
, то n является m-самовлюблённым числом. Если, сверх того, m = k, то n можно назвать истинным числом Армстронга.Очевидно, что при любом m может существовать лишь конечное число m-самовлюблённых чисел, так как, начиная с некоторого k
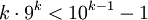 .
.Упоминания в литературе
В «Апологии математика» (A Mathematician’s Apology), Г. Харди писал:
«Есть только четыре числа, исключая единицу, которые равны сумме кубов своих цифр:
153 = 13 + 53 + 33
370 = 33 + 73 + 03
371 = 33 + 73 + 13
и 407 = 43 + 03 + 73. Это необычный факт, очень удобный для головоломных разделов в газетах и для развлечения любителей, но в нём нет ничего, что бы привлекало к нему математиков»Числа Армстронга в различных системах счисления
- Начальные числа Армстронга в десятичной системе счисления:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, … (последовательность A005188 в OEIS).
- В системе с основанием 3:
- В системе с основанием 4:
Программа для получения чисел Армстронга
На языке
nums = 1 puts('To what number?') f1 = gets.chomp.to_i while (nums <= f1) num1=nums num2=nums num3=nums mass=[ ] len=num3.to_s.length k=len while (k >= 1) g=(num3 - num3%(10**(k-1)))/(10**(k-1)) mass.push(g) num3=num3%(10**(k-1)) k=k-1 end f = 0 while f <= mass.length num1 = num1 - (mass[f].to_i**len.to_i) f=f+1 end if num1 == 0 puts( num2.to_s + ' - Armstrong number') end nums = nums + 1 end
Похожие классы чисел
Иногда термином «самовлюблённые числа» называют любой тип чисел, которые равны некоторому выражению от их собственных цифр. Например, таковыми могут быть: совершенные и дружественные числа, числа Брауна, числа Фридмана, счастливые билеты и т. п.
Литература
- Joseph S. Madachy, Mathematics on Vacation, Thomas Nelson & Sons Ltd. 1966, стр. 163—175.
Внешние ссылки
- Статья про самовлюблённые числа на сайте Wolfram Math World (англ.)
- Narcissistic Numbers(англ.)
- Digital Invariants(англ.)
См. также
Wikimedia Foundation. 2010.
