- Рамануджан, Сриниваса Айенгор
-
 Один из немногих известных портретов С. Рамануджана
Один из немногих известных портретов С. РамануджанаРамануджан Сриниваса Айенгор (Ramanujan) (22 декабря 1887, Ироду на юге Индии, — 26 апреля 1920, близ Мадраса) — индийский математик.
Не имея специального математического образования, получил замечательные результаты в области теории чисел. Наиболее значительна его работа совместно с Г. Харди по асимптотике функции p(n) — числа представлений числа n суммой положительных слагаемых.
Сфера его интересов очень широка. Это магические квадраты, квадратура круга, бесконечные ряды, круглые числа (то есть числа, являющиеся произведениями значительного количества малых сомножителей), разбиения, гипергеометрические ряды, функции и специальные суммы, носящие его имя, определённые интегралы, эллиптические и модулярные функции.
Он нашел несколько частных решений уравнения Эйлера (см. задача о четырех кубах), сформулировал около 120 теорем (в основном в виде исключительно сложных тождеств). Современные математики считают, что Рамануджан был и остается крупнейшим знатоком цепных дробей в мире.
Одним из самых замечательных результатов Рамануджана в этой области является формула, в соответствии с которой сумма простого числового ряда с цепной дробью в точности равна выражению, в котором присутствует произведение e на π:
Математикам хорошо известна формула вычисления числа π, полученная Рамануджаном в 1910 году путём разложения арктангенса в ряд Тейлора:
Всего при k = 100 достигается невиданная ранее точность вычисления мировой константы — шестьсот верных значащих цифр!
Пример бесконечной суммы, найденной Рамануджаном:
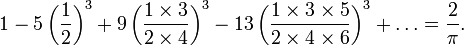
Эта удивительная формула — одна из предложенных им к первому письму Харди. Каким образом, сумма знакочередующего ряда может вдруг оказаться равной 2 / π, Харди долго не мог понять. Доказательство точного равенства неэлементарно.
Формулы Рамануджана удивительно изящны:
По поводу ряда открытий индийского математика есть остроумное замечание: «Они должны быть истинными, поскольку если бы они не были истинными, то ни у кого не хватило бы воображения, чтобы изобрести их».
Сам Рамануджан говорил, что формулы ему во сне внушает богиня Намаджири (Namagiri, Намаккаль). Эти формулы иногда всплывают в современнейших разделах науки, о которых в его время никто даже не догадывался.
Чтобы сохранить наследие этого удивительного, ни на кого не похожего математика, была издана книга, в которой приведены просто фотокопии его черновиков.
Понятия, связанные с именем Рамануджана
Рамануджан внёс значительный вклад в математику. Его имя носят:
- Гипотеза Рамануджана
- Суммы Рамануджана
- Функция Рамануджана
- Число Рамануджана — Харди
- Тождество Роджерса — Рамануджана
- Теорема Харди — Рамануджана
- Тождество Доугалла — Рамануджана
Литература
- С. Г. Гиндикин Рассказы о физиках и математиках. — издание третье, расширенное. — М.: МЦНМО, 2001. — ISBN 5-900916-83-9
- Г. Харди «Двенадцать лекций о Рамануджане». М.: Институт компьютерных исследований, 2002, с. 336.
- С. Г. Гиндикин Загадка Рамануджана // Квант. — 1987. — № 10. — С. 14.
- Р. Аски «С. Рамануджан. Гипергеометрические и базисные гипергеометрические ряды».
- Дж. Борвейн, П. Борвейн Рамануджан и число π // В мире науки. — 1988. — № 4.
- В. И. Левин «Рамануджан — математический гений Индии» (альтернативная ссылка). М.: «Знание», 1968.
- В. И. Левин «Жизнь и творчество индийского математика С. Рамануджана», «Историко-математические исследования», 1960.
- Дж. И. Литлвуд «Математическая смесь».
- Литература о Рамануджане в рунете
Wikimedia Foundation. 2010.

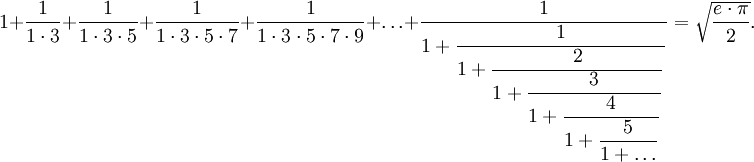
![\pi = \frac{9801}{2\sqrt{2} \sum\limits^\infty_{k=0} \displaystyle\frac{(4k)!}{(k!)^4} \times \displaystyle\frac{[1103 + 26390k]}{(4 \times 99)^{4k}}}.](/pictures/wiki/files/53/5398535e4845ddb6a69d60a29333c999.png)