- Чехстоунова компактификация
-
В общей топологии компактификация — операция, которая преобразует произвольные топологические пространства в компактные.
Формально компактификация пространства X определяется как пара
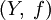 , где Y компактно,
, где Y компактно, 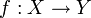 гомеоморфизм на свой образ f(X) и f(X) плотно в Y.
гомеоморфизм на свой образ f(X) и f(X) плотно в Y.На компактификациях некоторого фиксированного пространства X можно ввести частичный порядок. Положим
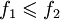 для двух компактификаций
для двух компактификаций 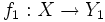 ,
, 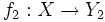 , если существует непрерывное отображение
, если существует непрерывное отображение 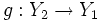 такое, что gf2 = f1. Максимальный (с точностью до гомеоморфизма) элемент в этом порядке называется компактификацией Стоуна — Чеха[1] и обозначается βX. Для того, чтобы у пространства X существовала компактификация Стоуна — Чеха, удовлетворяющая аксиоме отделимости Хаусдорфа, достаточно, чтобы X удовлетворяло аксиоме отделимости
такое, что gf2 = f1. Максимальный (с точностью до гомеоморфизма) элемент в этом порядке называется компактификацией Стоуна — Чеха[1] и обозначается βX. Для того, чтобы у пространства X существовала компактификация Стоуна — Чеха, удовлетворяющая аксиоме отделимости Хаусдорфа, достаточно, чтобы X удовлетворяло аксиоме отделимости 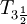 .
.Одноточечная компактификация (или компактификация Александрова) устроена следующим образом. Пусть
 и открытыми множествами в Y считаются все открытые множества X, а также множества вида
и открытыми множествами в Y считаются все открытые множества X, а также множества вида 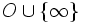 , где
, где 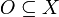 имеет компактное (в X) дополнение. f берётся как естественное вложение X в Y.
имеет компактное (в X) дополнение. f берётся как естественное вложение X в Y. 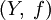 тогда компактификация, причём Y хаусдорфово тогда и только тогда, когда X хаусдорфово и локально компактно.
тогда компактификация, причём Y хаусдорфово тогда и только тогда, когда X хаусдорфово и локально компактно.Примеры одноточечной компактификации
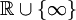 с топологией, сконструированной как указано выше, является компактным пространством. Не трудно доказать, что если два пространства гомеоморфны, то и соотвествующие одноточечные компактификации гомеоморфны. В частности, так как окружность на плоскости без одной точки гомеоморфна с
с топологией, сконструированной как указано выше, является компактным пространством. Не трудно доказать, что если два пространства гомеоморфны, то и соотвествующие одноточечные компактификации гомеоморфны. В частности, так как окружность на плоскости без одной точки гомеоморфна с 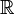 (пример гомеоморфизма — стереографическая проекция), целая окружность гомеоморфна с
(пример гомеоморфизма — стереографическая проекция), целая окружность гомеоморфна с 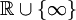 . Аналогично,
. Аналогично, 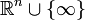 гомеоморфно c n-мерной гиперсферой.
гомеоморфно c n-мерной гиперсферой.Примечания
- ↑ Также «стоунчеховская компактификация» и «чехстоунова компактификация».
Wikimedia Foundation. 2010.
