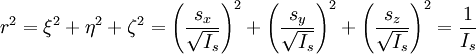Центробежный момент инерции

Момент инерции — скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Осевой момент инерции

Моментом инерции механической системы относительно неподвижной оси a («осевой момент инерции») называется физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

$J_a=\sum_{i=1}^n m_i r_i^2\,\!$,

где:

• m_i — масса i-й точки,
• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.

$J_a=\int\limits_{(m)} r^2dm=\int\limits_{(V)} \rho r^2dV\,\!$,

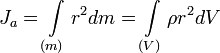где:

• dm = ρdV — масса малого элемента объёма тела dV,
• ρ — плотность,
• r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

$J_a=D\int\limits_{(V)} r^2dV\,\!$

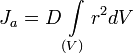
Теорема Гюйгенса-Штейнера

Основная статья: Теорема Штейнера

Момент инерции данного тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

$J=J_c+md^2\,\!$

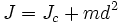
Если 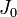$~J_0$ — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии 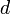$~d$ от неё, равен

$~J=J_0+md^2$,

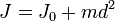где 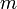$~m$ — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

$~J=J_0+md^2=\frac{1}{12}ml^2+m\left(\frac{l}{2}\right)^2=\frac{1}{3}ml^2$

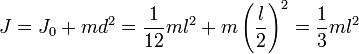
Осевые моменты инерции некоторых тел

Моменты инерции однородных тел простейшей формы относительно некоторых осей

Тело	Положение оси a	Момент инерции Ja
Полый тонкостенный цилиндр (кольцо) радиуса R и массы m	Ось цилиндра	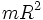$~mR^2$
Сплошной цилиндр (диск) радиуса R и массы m	Ось цилиндра	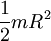$\frac{1}{2}mR^2$
Шар радиуса R и массы m	Ось проходит через центр шара	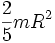$\frac{2}{5}mR^2$
Тонкостенная сфера радиуса R и массы m	Ось проходит через центр сферы	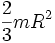$\frac{2}{3}mR^2$
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его середину	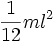$\frac{1}{12}ml^2$
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец	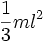$\frac{1}{3}ml^2$

Центробежный момент инерции

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:

$J_{xy}=\int\limits_{(m)} xydm=\int\limits_{(V)} xy\rho dV\,\!$

$J_{xz}=\int\limits_{(m)} xzdm=\int\limits_{(V)} xz\rho dV\,\!$

$J_{yz}=\int\limits_{(m)} yzdm=\int\limits_{(V)} yz\rho dV\,\!$

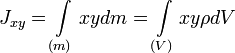
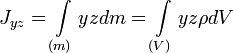
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции J_xy и J_xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.

Геометрический момент инерции

Геометрический момент инерции — геометрическая характеристика сечения, пропорциональная площади сечения и квадратно пропорциональная расстоянию до этого сечения. Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости и взаимного расположения различных элементов конструкции.

Геометрический момент инерции двух стержней диаметром d на расстоянии L:

J = 2dL²

Центральный момент инерции

Центральный момент инерции 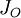$~J_O$ (или момент инерции относительно точки O) — это величина

$J_a=\int\limits_{(m)} r^2dm=\int\limits_{(V)} \rho r^2dV\,\!$,

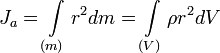где:

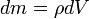• $~dm=\rho dV$ — масса малого элемента объёма тела dV,
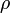• $~\rho$ — плотность,
• $~r$ — расстояние от элемента dV до точки O.

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: $~J_O=J_{xy}+J_{yz}+J_{xz}=\frac{1}{2}\left(J_x+J_y+J_z\right)$.

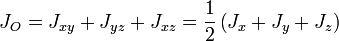Тензор инерции и эллипсоид инерции

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором 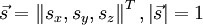$~\vec s = \left \Vert s_x , s_y , s_z \right \Vert^T ,\left \vert \vec s \right \vert=1$, можно представить в виде квадратичной (билинейной) формы :

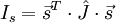$~ I_s= \vec s^T \cdot \hat J \cdot \vec s \qquad$ (1),

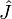где $~ \hat J$ — тензор инерции. Матрица тензора инерции симметрична, имеет размеры 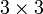$~ 3 \times 3$ и состоит из компонент центробежных моментов:

$~ \hat J = \left \Vert \begin{array}{ccc} J_{xx} & -J_{xy} & -J_{xz} \\ -J_{yx} & J_{yy} & -J_{yz} \\-J_{zx} & -J_{zy} & J_{zz} \end{array} \right \Vert$ , $~ J_{xy}= J_{yx}, J_{xz}= J_{zx}, J_{zy}= J_{yz},$
$~J_{xx}=\int\limits_{(m)} (y^2+z^2)dm , J_{yy}=\int\limits_{(m)} (x^2+z^2)dm, J_{zz}=\int\limits_{(m)} (x^2+y^2)dm$

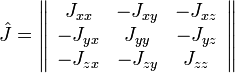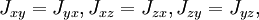
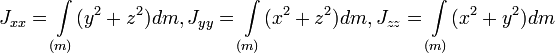
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора $~ \hat J$:
$~ \hat J_d = \hat Q^T \cdot \hat J \cdot \hat Q ;$ $~ \hat J_d = \left \Vert \begin{array}{ccc} J_{X} & 0 & 0 \\ 0 & J_{Y} & 0 \\0 & 0 & J_{Z} \end{array} \right \Vert$
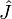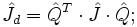
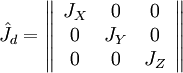
Где,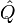 $~ \hat Q$ — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины $~ J_{X},J_{Y},J_{Z}$ — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

$~ I_s= J_{X} \cdot s_x^2 +J_{Y} \cdot s_y^2 + J_{Z} \cdot s_z^2$.

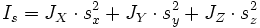Откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на $~ I_s$

$~ \left ( {s_x \over \sqrt {I_s}}\right )^2 \cdot J_{X} + \left ( {s_y \over \sqrt {I_s}}\right )^2 \cdot J_{Y} + \left ( {s_z \over \sqrt {I_s}}\right )^2 \cdot J_{Z} =1$

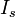
и произведя замены:

$~ \xi= {s_x \over \sqrt {I_s}}, \eta= {s_y \over \sqrt {I_s}}, \zeta= {s_z \over \sqrt {I_s}}$,

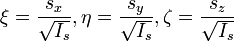получаем канонический вид уравнения эллипсоида в координатах $~ \xi \eta \zeta$:

$~ \xi^2 \cdot J_{X} + \eta^2 \cdot J_{Y} + \zeta^2 \cdot J_{Z} =1$

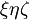Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой проходящей через центр эллипсоида и эту точку:

$~ r^2 = \xi^2 + \eta^2 + \zeta^2 = \left ( {s_x \over \sqrt {I_s}}\right )^2 + \left ( {s_y \over \sqrt {I_s}}\right )^2 + \left ( {s_z \over \sqrt {I_s}}\right )^2 = {1 \over I_s}$

См. также

• Классическая механика
• Инерция
• Метод главных компонент
• Сопротивление материалов
• Теорема Штейнера
• Список моментов инерции (англ.)
• Список тензоров инерции (англ.)

Литература

• Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
• Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
• Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
• Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
• Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm

Ссылки