Функция Макдональда

Модифици́рованные фу́нкции Бе́сселя - это функции Бесселя от мнимого аргумента.

Если в дифференциальном уравненни Бесселя

$z^2 \frac{d^2 \omega}{dz^2} + z \frac{d\omega}{dz} + (z^2 - \nu^2)\omega = 0$

заменить 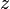$\ z$ на $\ iz$, оно примет вид

$z^2 \frac{d^2 \omega}{dz^2} + z \frac{d\omega}{dz} - (z^2 + \nu^2)\omega = 0, \qquad (1)$

Это уравнение называется модифицированным уравнением Бесселя

Если 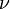$~\nu$ не является целым числом, то функции Бесселя $~J_\nu(iz)$ и $~J_{-\nu}(iz)$ являются двумя линейно независимыми решениями уравнения $~(1)$, однако чаще используют функции

$I_\nu(z)=e^{-\frac{i\nu\pi}{2}}J_ \nu \left( z e^{\frac{i\pi}{2}}\right)=\sum^\infty_{k=0}\frac{\left( \dfrac{z}{2} \right)^{2k+\nu}}{k!\Gamma(k+\nu+1)}$ и $~I_{-\nu}(z).$

Их называют модифицированными функциями Бесселя первого рода . Если 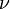$~\nu$ — вещественное число, а 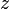$~z$ — положительно эти функции принимают вещественные значения.

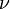$~\nu$ называется порядком функции.

Функция

$~K_\nu(z)=\frac{\pi}{2\sin \nu\pi}\biggl[I_\nu(z)-I_{-\nu}(z)\biggr]$

также является решением уравнения $~(1)$. Её называют модифицированной функцией Бесселя второго рода или функцией Макдональда . очевидно, что

$~K_\nu(z)=K_{-\nu}(z)$

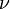и принимает вещественные значения, если $~\nu$ — вещественное число, а 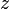$~z$ — положительно.

График модифицированных функций Бесселя первого рода с различными порядками

График модифицированных функций Бесселя второго рода с различными порядками

Функции целого порядка

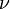Так как $~I_{-\nu}(z)=I_\nu (z)$ при целом $~\nu$ в качестве фундаментальной системы решений уравнения 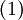$~(1)$ выбирают $~I_n (z)$ и $~K_n (z),$ где

$K_n(z)=\lim\limits_{\nu \to n}K_\nu(z)$

Рекуррентные соотношения и формулы дифференцирования

Модифицированные функции Бесселя первого рода

$~\left(\frac{d}{zdz}\right)^m\Bigl[z^\nu I_\nu(z) \Bigr]=z^{\nu-m} I_{\nu-m}(z).$

$~\left(\frac{d}{zdz}\right)^m\Bigl[z^{-\nu} I_\nu(z) \Bigr]=z^{-\nu-m} I_{\nu+m}(z).$

$~I_{\nu-1}(z)-I_{\nu+1}(z)=2\nu z^{-1} I_\nu(z).$

$~I_{\nu-1}(z)+I_{\nu+1}(z)=2I'_\nu(z).$

Модифицированные функции Бесселя второго рода

$~\left(\frac{d}{zdz}\right)^m\Bigl[z^\nu K_\nu(z) \Bigr]=(-1)^m z^{\nu-m} K_{\nu-m}(z).$

$~\left(\frac{d}{zdz}\right)^m\Bigl[z^{-\nu} K_\nu(z) \Bigr]=(-1)^m z^{-\nu-m} K_{\nu+m}(z).$

$~K_{\nu-1}(z)-K_{\nu+1}(z)=-2\nu z^{-1} K_\nu(z).$

$~K_{\nu-1}(z)+K_{\nu+1}(z)=-2K'_\nu(z).$

Вронскиан системы модифицированных функций Бесселя

$W\left[I_\nu(z),I_{-\nu}(z)\right]=-\frac{2\sin(\nu\pi)}{\pi z}.$

$W\left[I_\nu(z),K_\nu (z)\right]=z^{-1}.$

Интегральные представления

Модифицированные функции Бесселя первого рода

$I_\nu (z)=\frac{2^{-\nu}z^\nu}{\sqrt{\pi}\Gamma(\nu+\frac12)}\int_0^\pi e^{z\cos t}\left(\sin t\right)^{2\nu} dt, \qquad Re(\nu)>-\frac12, \Gamma(z)$ — гамма-функция.

$I_\nu (z)=\frac{2^{1-\nu}z^\nu}{\sqrt{\pi}\Gamma(\nu+\frac12)}\int_0^1 (1-t^2)^{\nu-\frac12}\cosh(zt) dt, \qquad Re(\nu)>-\frac12.$

$I_\nu (z)=\frac{2^{-\nu}z^\nu}{\sqrt{\pi}\Gamma(\nu+\frac12)}\int_{-1}^1 (1-t^2)^{\nu-\frac12} e^{-zt} dt, \qquad Re(\nu)>-\frac12.$

$I_n(z)=\frac{1}{\pi}\int_0^\pi e^{z\cos t}\cos (nt)dt, \qquad n \in \mathbb Z, Re(z)>0.$

Модифицированные функции Бесселя второго рода

$K_\nu(z)=\int_0^\infty e^{-z\cosh t}\cosh (\nu t)dt, \qquad Re(z)>0.$

$K_\nu (z)=\frac{\sqrt{\pi}z^\nu}{\Gamma(\nu+\frac12)}\int_1^\infty (t^2-1)^{\nu-\frac12}e^{-zt} dt, \qquad Re(\nu)>-\frac12, Re(z)>0.$

$K_\nu (z)=\frac{\sqrt{\pi}z^\nu}{\Gamma(\nu+\frac12)}\int_0^\infty e^{-z\cosh t}\left(\sinh t \right)^{2\nu} dt, \qquad Re(\nu)>-\frac12, Re(z)>0.$

Асимптотическое поведение

$I_\nu(z)\varpropto \frac{e^z}{\sqrt{2\pi z}}\left(1+O\left(\frac{1}{z} \right) \right), \qquad \left|Arg(z)\right|<\frac{\pi}{2},\left|z\right| \to \infty.$

$K_\nu(z)\varpropto \sqrt{\frac{\pi}{2}}\frac{e^{-z}}{\sqrt{z}}\left(1+O\left(\frac{1}{z} \right) \right), \qquad \left|z\right| \to \infty.$

См. также

• Цилиндрические функции

Литература

• Ватсон Г., Теория бесселевых функций т. 1,2 М., ИЛ, 1949 г.
• Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Функции Бесселя, функции параболического цилиндра, отогональные многочлены Справочная математическая библиотека М. Физматгиз 1966 г. 296 с.

Внешние ссылки

• MathWorld description of Modified Bessel Function of the First Kind
• MathWorld description of Modified Bessel Function of the Second Kind