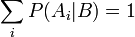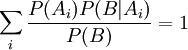Формула Байеса

Теорема Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность наступления события в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях. По формуле Байеса можно более точно пересчитывать вероятность, беря в учёт как ранее известную информацию, так и данные новых наблюдений.

Формулировка

Формула Байеса: 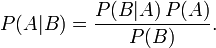$P(A|B) = \frac{P(B | A)\, P(A)}{P(B)}.$, где P(A) — априорная вероятность гипотезы A (смысл такой терминологии см. ниже); P(A | B) — вероятность гипотезы A при наступлении события B (апостериорная вероятность); P(B | A) — вероятность наступления события B при истинности гипотезы A; P(B) — вероятность наступления события B.

Вывод формулы  

Формула элементарно выводится из определения условной вероятности: $P(A|B) = \frac{P(AB)}{P(B)} \Rightarrow P(AB) = P(A|B)P(B) = P(B|A)P(A)$

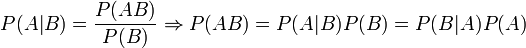
«Физический смысл» и терминология

Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной.

События, отражающие действие «причин», в данном случае обычно называют гипотезами, так как они — предполагаемые события, повлекшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную - с учетом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учетом данных о событии).

Следствие

Важным следствием формулы Байеса является формула полной вероятности события, зависящего от нескольких несовместных гипотез (и только от них!).

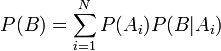$P(B)=\sum_{i=1}^N P(A_i)P(B|A_i)$ — вероятность наступления события B, зависящего от ряда гипотез A_i, если известны степени достоверности этих гипотез (например, измерены экспериментально);

Вывод формулы  

Если событие зависит только от причин A_i, то если оно произошло, значит, обязательно произошла какая-то из причин, т.е.

$\sum_i P(A_i|B) = 1\,$

По формуле Байеса

$\sum_i \frac{P(A_i)P(B|A_i)}{P(B)} = 1$

Переносом P(B) вправо получаем искомое выражение.

Метод фильтрации спама

Метод, основанный на теореме Байеса, нашел успешное применение в фильтрации спама.

Описание

При обучении фильтра для каждого встреченного в письмах слова высчитывается и сохраняется его «вес» — вероятность того, что письмо с этим словом — спам (в простейшем случае — по классическому определению вероятности: «появлений в спаме / появлений всего»^[1]).

При проверке вновь пришедшего письма вычисляется вероятность того, что оно — спам, по указанной выше формуле для множества гипотез. В данном случае «гипотезы» — это слова, и для каждого слова «достоверность гипотезы» 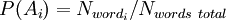$P(A_i) = N_{word_i}/N_{words~total}$ — % этого слова в письме, а «зависимость события от гипотезы» P(B | A_i) — вычисленнный ранее «вес» слова. То есть «вес» письма в данном случае — не что иное, как усредненный «вес» всех его слов.

Отнесение письма к «спаму» или «не-спаму» производится по тому, превышает ли его «вес» некую планку, заданную пользователем (обычно берут 60-80 %). После принятия решения по письму в базе данных обновляются «веса» для вошедших в него слов.

Характеристика

Данный метод прост (алгоритмы элементарны), удобен (позволяет обходиться без «черных списков» и подобных искусственных приемов), эффективен (после обучения на достаточно большой выборке отсекает до 95—97 % спама, и в случае любых ошибок его можно дообучать). В общем, есть все показания для его повсеместного использования, что и имеет место на практике — на его основе построены практически все современные спам-фильтры.

Впрочем, у метода есть и принципиальный недостаток: он базируется на предположении, что одни слова чаще встречаются в спаме, а другие — в обычных письмах, и неэффективен, если данное предположение неверно. Впрочем, как показывает практика, такой спам даже человек не в состоянии определить «на глаз» — только прочтя письмо и поняв его смысл.

Еще один, не принципиальный, недостаток, связанный с реализацией — метод работает только с текстом. Зная об этом ограничении, спамеры стали вкладывать рекламную информацию в картинку, текст же в письме либо отсутствует, либо не несет смысла. Против этого приходится пользоваться либо средствами распознавания текста («дорогая» процедура, применяется только при крайней необходимости), либо старыми методами фильтрации — «черные списки» и регулярные выражения (так как такие письма часто имеют стереотипную форму).

См. также

• Условная вероятность
• Парадокс Монти Холла
• Некорректное априорное распределение
• Байесовская сеть доверия

Примечания

1. ↑ В более сложных случаях возможна предварительная обработка текста: приведение слов в начальную форму, удаление служебных слов, вычисление «веса» для целых фраз, транслитерация и пр.

Ссылки

• http://osu.cctpu.edu.ru/GOSY/ES/es_9.htm
• http://teorver-online.narod.ru/teorver10.html

Литература

• Берд Киви. Теорема преподобного Байеса. // Журнал «Компьютерра», 24 августа 2001 г.
• Paul Graham. A plan for spam (англ.). // Персональный сайт Paul Graham.