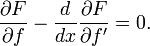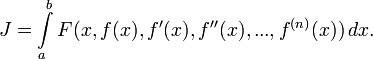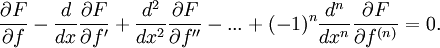- Уравнения Эйлера-Лагранжа
-
Уравнения Эйлера — Лагранжа являются основными формулами вариационного исчисления, c помощью которых ищутся экстремумы функционалов. В частности, эти уравнения широко используются в задачах оптимизации, и, совместно с принципом действия, используются для вычисления траекторий. Уравнение в некотором смысле сходно с теоремой дифференциального исчисления, утверждающей, что в точке, где первая производная функции обращается в нуль, функция достигает экстремума.
Уравнения были получены Леонардом Эйлером и Жозефом-Луи Лагранжем в 1750-х годах.
Содержание
Утверждение
Пусть задан функционал
с подинтегральной функцией
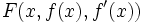 , обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом. Если этот функционал достигает экстремума на некоторой функции
, обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом. Если этот функционал достигает экстремума на некоторой функции 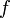 , то для неё должно выполняться обыкновенное дифференциальное уравнение
, то для неё должно выполняться обыкновенное дифференциальное уравнениекоторое называется уравнением Эйлера — Лагранжа.
Примеры
Рассмотрим стандартный пример: найти кратчайший путь между двумя точками плоскости. Ответом, очевидно, является отрезок, соединяющий эти точки. Попробуем получить его с помощью уравнения Эйлера — Лагранжа. Пусть точки, которые надо соединить, имеют координаты
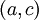 и
и 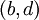 . Тогда длина пути
. Тогда длина пути 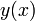 , соединяющего эти точки, может быть записана следующим образом:
, соединяющего эти точки, может быть записана следующим образом:Уравнение Эйлера — Ланранжа для этого функционала принимает вид:
откуда получаем, что
Таким образом, получаем прямую линию. Учитывая, что
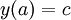 ,
, 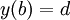 , т. е. что она проходит через исходные точки, получаем верный ответ: отрезок, соединяющий точки.
, т. е. что она проходит через исходные точки, получаем верный ответ: отрезок, соединяющий точки.Многомерные вариации
Существует также множество многомерных вариантов уравнений Эйлера — Лагранжа. Если q(t) — путь в n-мерном пространстве, то он доставляет экстремум функционалу
только если удовлетворяет условию
Эта формулировка особенно полезна, когда
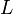 является лагранжианом, поскольку результирующие уравнения — уравнения движения.
является лагранжианом, поскольку результирующие уравнения — уравнения движения.Другое многомерное обобщение получается при рассмотрении функции n переменных. Если
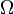 — какая-либо поверхность, то
— какая-либо поверхность, тодоставляет экстремум если только f удовлетворяет уравнению в частных производных
Если n = 2 и L — функционал энергии, то эта задача называется «минимизацией поверхности мыльной плёнки».
История
Уравнение Эйлера — Лагранжа было получено в 1750-х годах Эйлером и Лагранжем при решении задачи об изохроне. Это проблема определения кривой, по которой тяжёлая частица попадает в фиксированную точку за фиксированное время, независимо от начальной точки.
Лагранж решил эту задачу в 1755 году и отослал решение Эйлеру. Развитый впоследствии метод Лагранжа и применение его в механике привело к формулировке лагранжевой механики. Переписка учёных привела к созданию вариационного исчисления (термин придумал Эйлер в 1766 году).
Доказательство
Вывод одномерного уравнения Эйлера — Лагранжа является одним из классических доказательств в математике. Оно основывается на основной лемме вариационного исчисления.
Мы хотим найти такую функцию
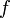 , которая удовлетворяет граничным условиям
, которая удовлетворяет граничным условиям 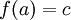 ,
, 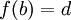 и доставляет экстремум функционалу
и доставляет экстремум функционалуПредположим, что
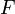 имеет непрерывные первые производные. Достаточно и более слабых условий, но доказательство для общего случая более сложно.
имеет непрерывные первые производные. Достаточно и более слабых условий, но доказательство для общего случая более сложно.Если
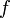 даёт экстремум функционалу и удовлетворяет граничным условиям, то любое слабое возмущение
даёт экстремум функционалу и удовлетворяет граничным условиям, то любое слабое возмущение 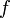 , которое сохраняет граничные условия, должно увеличивать значение
, которое сохраняет граничные условия, должно увеличивать значение 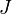 (если
(если 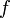 минимизирует его) или уменьшать
минимизирует его) или уменьшать 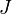 (если
(если 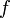 максимизирует).
максимизирует).Пусть
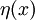 — любая дифференцируемая функция, удовлетворяющая условию
— любая дифференцируемая функция, удовлетворяющая условию 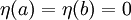 . Определим
. ОпределимПоскольку
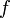 даёт экстремум для
даёт экстремум для 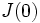 , то
, то 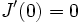 , то есть
, то естьИнтегрируя по частям второе слагаемое, находим, что
Используя граничные условия на
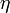 , получим
, получимОтсюда, так как
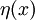 — любая, следует уравнение Эйлера — Лагранжа:
— любая, следует уравнение Эйлера — Лагранжа:Обобщение на случай с высшими производными
Лагранжиан может также зависеть и от призводных f порядка выше, чем первый.
Пусть функционал, экстремум которого нужно найти, задан в виде:
Если наложить граничные условия на f и на её производные до порядка n − 1 включительно, а также предположить, что F имеет непрерывные первые производные, то можно, применяя интегрирование по частям несколько раз, вывести уравнение Эйлера-Лагранжа и для этого случая:
См. также
Ссылки
- Weisstein, Eric W. Euler-Lagrange на сайте Wolfram MathWorld.(англ.)
- Calculus of Variations на сайте (англ.)
- Summary with some historical information
- Examples — задачи из вариационного исчисления.
Wikimedia Foundation. 2010.

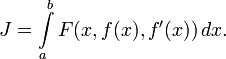
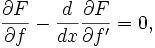
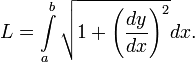
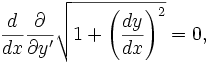
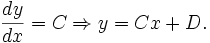
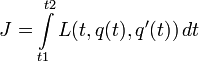
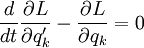
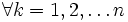
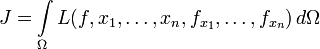
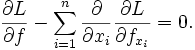
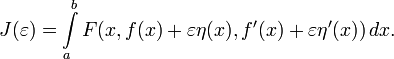
![J'(0) = \int\limits_a^b \left[ \eta(x) \frac{\partial F}{\partial f} + \eta'(x) \frac{\partial F}{\partial f'} \right]\,dx = 0.](/pictures/wiki/files/48/04b0f894b328707c8966052b4687e05c.png)
![0 = \int\limits_a^b \left[ \frac{\partial F}{\partial f} - \frac{d}{dx} \frac{\partial F}{\partial f'} \right] \eta(x)\,dx + \left[ \eta(x) \frac{\partial F}{\partial f'} \right]_a^b.](/pictures/wiki/files/102/f048db46ddcf255543e12c543cff0f96.png)
![0 = \int\limits_a^b \left[ \frac{\partial F}{\partial f} - \frac{d}{dx} \frac{\partial F}{\partial f'} \right] \eta(x)\,dx.](/pictures/wiki/files/50/2f9368afbb01e8f1904129413a3a05ad.png)