ЭЙЛЕРА -ЛАГРАНЖА УРАВНЕНИЕ

ЭЙЛЕРА -ЛАГРАНЖА УРАВНЕНИЕ

- необходимое условие экстремума в задачах вариационного исчисления, полученное Л. Эйлером в 1744. Впоследствии, используя другой метод, это ур-ние вывел Ж. Лагранж (J. Lagrange) в 1759.

Пусть поставлена задача вариац. исчисления, состоящая в определении экстремума функционала

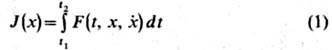
при известных условиях на концах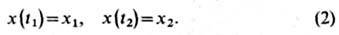

И пусть непрерывно дифференцируемая ф-ция x(t), 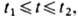есть решение задачи (1), (2). Тогда x(t )удовлетворяет Э.- Л. у.: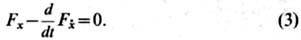

Ур-ние (3) можно записать в развёрнутом виде:

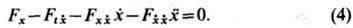
Гладкое решение ур-ния (3) [или (4)] наз. экстремалью. Если F_xx=0 в точке (t, х), лежащей на экстремали, то в этой точке экстремаль имеет непрерывную 2-ю производную х. Экстремаль, во всех точках к-рой 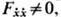наз. неособенной. Для неособенной экстремали Э.- Л. у. можно записать в виде, разрешённом относительно 2-й производной х.

Решение вариац. задачи (1), (2) необязательно должно быть непрерывно дифференцируемым. В общем случае оптимальное решение x(t) может быть кусочно дифференцируемой ф-цией. Тогда в угл. точках х(t) должны выполняться необходимые условия Вейерштрасса - Эрдмана, обеспечивающие непрерывность при переходе через угл. точку выражений 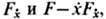а на отрезках между соседними угл. точками ф-ция 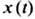должна удовлетворять

Э.-Л. у. Кусочно гладкие линии, составленные из кусков экстремалей и удовлетворяющие в угл. точках условиям Вейерштрасса-Эрдмана, наз. ломаными экстремалями.

В общем случае дифференциальное Э.- Л. у. является ур-нием 2-го порядка и, следовательно, его общее решение зависит от двух произвольных постоянных

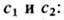
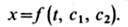
Эти произвольные постоянные можно определить из граничных условий (2):

Если рассматривается функционал, зависящий от неск. ф-ций,

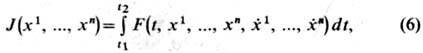
то вместо одного Э.- Л. у. приходят к системе n Э.-Л. у.:

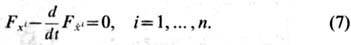
Общее решение системы (7) зависит от 2n произвольных постоянных, к-рые определяются из заданных 2n граничных условий (для задачи с закреплёнными концами).

В случае вариац. задач с подвижными концами, в к-рых левый и правый концы экстремали могут смещаться по нек-рым заданным гиперповерхностям, недостающие граничные условия, позволяющие получить замкнутую систему соотношений типа (5), определяются с помощью необходимого условия трансверсальности. Для простейшей задачи типа (1), в к-рой точка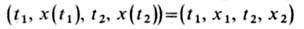

не фиксируется, а может принадлежать нек-рому множеству, условие трансверсальности записывается в виде

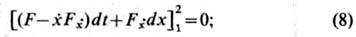оно должно выполняться при любых значениях дифференциалов dt₁ , dx₁ , dt₂ , dx₂ , удовлетворяющих проварьиро-ванным граничным условиям. Если левый и правый концы экстремали могут смещаться вдоль заданных линий 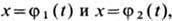то в силу условий

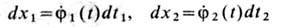и независимости вариаций dt₁ и dt₂ из (8) получают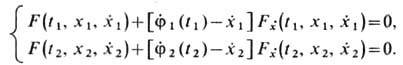

Если уравнения линий, вдоль к-рых смещаются левый и правый концы экстремали, заданы в неявном виде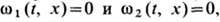 то условие трансверсальности записывается так: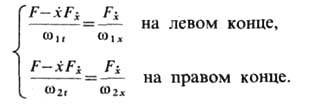

Если на один из концов экстремали не наложено никаких ограничений, то на этом конце в силу независимости соответствующих концевых вариаций dt и dx условие трансверсальности принимает вид

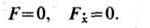
Для функционалов, содержащих производные высших порядков [а не только 1-го, как (1), (6)], необходимое условие, аналогичное Э.-Л. у., записывается в виде диф-ференц. ур-ния Эйлера-Пуассона (см. [1 ]).

Для вариац. задач, в к-рых разыскивается экстремум функционалов, зависящих от ф-ций неск. переменных, аналогичное необходимое условие записывается в виде ур-ния Эйлера - Остроградского, представляющего собой дифференц. ур-ние с частными производными (см. [2]).

В случае вариац. задач на условный экстремум получение системы Э.- Л. у. связано с использованием множителей Лагранжа. Напр., для т. н. задачи Больца, в к-рой требуется найти экстремум функционала, зависящего от n ф-ций
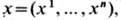
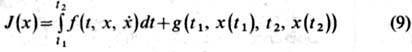при наличии дифференц. ограничений типа равенств 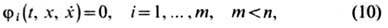и граничных условий 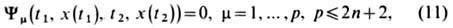с помощью множителей Лагранжа 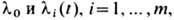из 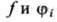составляется ф-ция 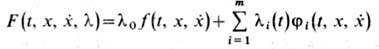и Э.-Л. у. записываются в виде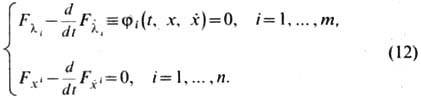

Т. <о., оптимальное решение вариац. задачи (9) - (11) должно удовлетворять системе (12), причём первые т из этих ур-ний совпадают с заданными условиями связи (10). Используя дополнительно необходимое условие трансверсальности, получают замкнутую краевую задачу для определения решения вариац. задачи (9) - (II).

Помимо Э.- Л. у. и условий трансверсальности оптимальное решение вариац. задачи должно удовлетворять и др. необходимым условиям [условию Клебша (Лежанд-ра), условию Вейерштрасса и условию Якоби].

Лит.:1)Ахиезер H. И., Лекции по вариационному исчислению, M., 1955; 2) Лаврентьев M. А., Люстерник Л. А., Курс вариационного исчисления, 2 изд., M.-Л., 1950.

И. Б. Вапн. <чрский.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.