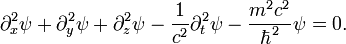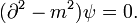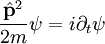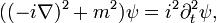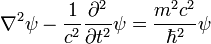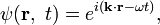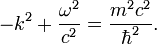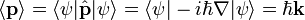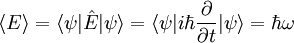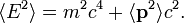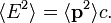- Уравнение Клейна-Гордона-Фока
-
Уравнение Клейна — Гордона (Уравнение Клейна — Гордона — Фока):
или, кратко, используя вдобавок естественные единицы (где
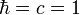 ):
):где
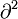 — оператор Д’Аламбера.
— оператор Д’Аламбера.— является релятивистской версией уравнения Шрёдингера. Используется для описания быстро движущихся частиц, имеющих массу (массу покоя). Строго применимо к описанию скалярных массивных полей (впрочем, пока с определенностью не известных в фундаментальной физике).
Кроме прочего, легко видеть, что уравнение Клейна — Гордона — Фока является обобщением волнового уравнения, подходящего для описания безмассовых скалярных и векторных полей.
Механические системы (реальные или воображаемые), описывающиеся уравнением Клейна — Гордона, могут быть простыми модификациями систем, описывающихся волновым уравнением, например:
- в одномерном случае — натянутая тяжелая нить, лежащая (приклеенная) на упругой (гуковской) подкладке.
- макроскопически изотропный кристалл, каждый атом которого находится, кроме связи с соседними атомами, еще и в фиксированной в пространстве квадратичной потенциальной яме.
- более реалистично, если говорить о реальных кристаллах, рассмотреть моды поперечных колебаний, при которых, например, соседние слои атомов колеблются в противофазе: такие моды (в линейном приближении) будут подчиняться двумерному уравнению Клейна — Гордона в координатах, лежащих в плоскости слоев.
Уравнение, в котором последний («массовый») член имеет знак, противоположный обычному, описывает в теоретической физике тахион. Такой вариант уравнения также допускает простую механическую реализацию.
Уравнение Клейна — Гордона для свободной частицы (которое и приведено выше) имеет простое решение в виде синусоидальных плоских волн.
- Замечание: положив пространственные производные нулю (что в квантовой механике соответствует нулевому импульсу частицы), мы имеем для обычного уравнения Клейна — Гордона гармонический осциллятор с частотой
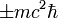 , что соответствует ненулевой энергии покоя, определяемой массой m частицы. Тахионный же вариант уравнения в этом случае неустойчив, а решение его включает в общем случае неограниченно возрастающую экспоненту.
, что соответствует ненулевой энергии покоя, определяемой массой m частицы. Тахионный же вариант уравнения в этом случае неустойчив, а решение его включает в общем случае неограниченно возрастающую экспоненту.
Содержание
История
Уравнение Клейна — Гордона первоначально записал Эрвин Шрёдингер до записи нерелятивистского уравнения, которое носит сейчас его имя. Он отказался от него, потому что не смог включить спин электрона в уравнение. Шрёдингер сделал упрощение уравнения Клейна — Гордона и нашёл «своё» уравнение.
В 1926 году, вскоре после публикации уравнения Шрёдингера, Фок написал статью о его обобщении на случай магнитных полей, где силы зависели от скорости и независимо вывел это уравнение. И Клейн, и Фок использовали метод Калуцы — Клейна. Фок также ввёл калибровочную теорию для волнового уравнения.
Вывод
- (Здесь использованы естественные единицы где
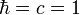 ).
).
Уравнение Шрёдингера для свободной частицы записывается так:
где
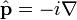 — оператор импульса, оператор же
— оператор импульса, оператор же 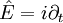 — будем называть, в отличие от гамильтониана, просто оператором энергии.
— будем называть, в отличие от гамильтониана, просто оператором энергии.Уравнение Шрёдингера не является релятивистски ковариантным, то есть не согласуется со специальной теорией относительности (СТО).
Используем релятивистское соотношение, связывающее энергию и импульс (из СТО):
- p2 + m2 = E2.
Тогда просто подставляя квантовомеханическиe оператор импульса и оператор энергии [1] — получаем:
что в ковариантной форме запишется так:
где
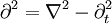 — оператор Д’Аламбера.
— оператор Д’Аламбера.Решение уравнения Клейна — Гордона для свободной частицы
Искать решение уравнения Клейна — Гордона для свободной частицы
можно, как и для любого линейного дифференциального уравнения с постоянными коэффициентами, в виде суперпозиции (то есть любой, конечной или бесконечной линейной комбинации) плоских волн:
подставляя же каждую такую волну в уравнение, получаем условие на
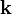 и ω:
и ω:Плоская волна, как легко заметить, описывает чистое состояние с определенной энергией и импульсом (то есть является собственной функцией соответствующих операторов). Энергия и импульс (то есть собственные значения этих операторов), исходя из этого, могут быть для нее просто посчитаны, как и в случае нерелятивистской частицы:
Найденное соотношение k и ω тогда (снова) дает уравнение связи между энергией и импульсом релятивистской частицы с ненулевой массой, известное из классики:
Причем легко видеть, что соотношение для средних величин будет выполняться не только для состояний с определенной энергией и импульсом, но и для любой их суперпозиции, то есть для любого решения уравнения Клейна — Гордона (что, в частности, обеспечивает выполнение этого соотношения и в классическом пределе).
Для безмассовых частиц мы можем положить m = 0 в последнем уравнении. Тогда получим для безмассовых частиц закон дисперсии (он же соотношение энергии и импульса) в виде:
Использовав формулу групповой скорости
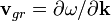 , нетрудно получить обычные релятивистские формулы связи импульса и энергии со скоростью; в принципе, того же результата можно добиться и просто посчитав коммутатор гамильтониана с координатой, но в случае уравнения Клейна — Гордона мы сталкиваемся с трудностью выписать гамильтониан в явном виде [2] (очевиден только квадрат гамильтониана).
, нетрудно получить обычные релятивистские формулы связи импульса и энергии со скоростью; в принципе, того же результата можно добиться и просто посчитав коммутатор гамильтониана с координатой, но в случае уравнения Клейна — Гордона мы сталкиваемся с трудностью выписать гамильтониан в явном виде [2] (очевиден только квадрат гамильтониана).Примечания
- ↑ Можно было бы просто извлечь корень из оператора в скобках в левой части уравнения
- ↑ см. примечание 1.
См. также
Внешние ссылки
- Линейное уравнение Клейна — Гордона на EqWorld: The World of Mathematical Equations.
- Нелинейное уравнение Клейна — Гордона на EqWorld: The World of Mathematical Equations.
Wikimedia Foundation. 2010.