КЛЕЙНА — ГОРДОНА — ФОКА УРАВНЕНИЕ
- КЛЕЙНА — ГОРДОНА — ФОКА УРАВНЕНИЕ
- КЛЕЙНА — ГОРДОНА — ФОКА УРАВНЕНИЕ
-
квантовое релятив. ур-ние для ч-ц с нулевым спином. Исторически К.— Г.— Ф. у. явл. первым релятив. ур-нием квант. механики для волн. ф-ции ч-цы (y); оно было предложено в 1926 австр. физиком Э. Шредингером (как релятив. обобщение Шредингера уравнения) и независимо от него швед. физиком 0. Клейном (О. Klein), В. А. Фоком, нем. физиком В. Гордоном (W. Gordon) и др. Для свободной ч-цы К.— Г.— Ф. у. записывается в виде:
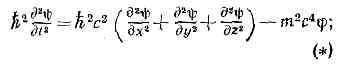
ему соответствует релятив. соотношение между энергией ?и импульсом р ч-цы: ?2=p2c3+m2c4 (m —
масса ч-цы). Решением ур-ния (*) явл. ф-ция y(х, у, z, t), зависящая только от координат (х, у, z) и времени (t). Следовательно, ч-цы, состояние к-рых описывается этой ф-цией, не обладают никакими дополнит. внутр. степенями свободы, т. е. действительно явл. бесспиновыми (к таким ч-цам относятся, напр., p- и К-мезоны).
Анализ ур-ния показал, что его решение (y) принципиально отличается по своему физ. смыслу от обычной волн. ф-ции как амплитуды
вероятности нахождения ч-цы в заданном месте пр-ва в заданный момент времени: y(х, у, z, t) не определяется однозначно значением y в нач. момент времени (такая однозначная зависимость постулируется в квант. механике), и, более того, выражение вероятности
состояния наряду с положит. значениями может принимать также и лишённые физ. смысла отрицат. значения. Поэтому сначала от К.— Г.— Ф. у. отказались. Однако в 1934 швейц. физик В. Паули и амер. физик В. Ф. Вайскопф нашли правильную интерпретацию этого ур-ния в рамках квантовой теории поля (они рассмотрели его как ур-ние поля, аналогичное ур-ниям Максвелла для эл.-магн. поля, и проквантовали; при этом y стало оператором).
Физический энциклопедический словарь. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1983.
.
Полезное
Смотреть что такое "КЛЕЙНА — ГОРДОНА — ФОКА УРАВНЕНИЕ" в других словарях:
Уравнение Клейна — Уравнение Клейна Гордона (Уравнение Клейна Гордона Фока, уравнение Клейна Фока): или, кратко, используя вдобавок естественные единицы (где ): где оператор Д’Аламбера. явля … Википедия
КЛЕЙНА - ГОРДОНА УРАВНЕНИЕ — (Клейна Гордона Фока уравнение) простейшее релятивистски инвариантное ур ние, описывающее свободное скалярное (или псевдоскалярное) поле физическое. Впервые получено в 1926 Э. Шрёдингеро … Физическая энциклопедия
Уравнение Клейна-Гордона-Фока — Уравнение Клейна Гордона (Уравнение Клейна Гордона Фока): или, кратко, используя вдобавок естественные единицы (где ): где оператор Д’Аламбера. является релятивистской версией … Википедия
Уравнение Клейна — Гордона — Фока — Уравнение Клейна Гордона (Уравнение Клейна Гордона Фока): или, кратко, используя вдобавок естественные единицы (где ): где оператор Д’Аламбера. является релятивистской версией … Википедия
Уравнение Клейна — Гордона — Уравнение Клейна Гордона (Уравнение Клейна Гордона Фока): или, кратко, используя вдобавок естественные единицы (где ): где … Википедия
Уравнение Клейна-Гордона — Уравнение Клейна Гордона (Уравнение Клейна Гордона Фока): или, кратко, используя вдобавок естественные единицы (где ): где оператор Д’Аламбера. является релятивистской версией … Википедия
Уравнение колебаний струны — Волновое уравнение в математике линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика,… … Википедия
Уравнение колебания струны — Волновое уравнение в математике линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика,… … Википедия
уравнение клейна-гордона-фока — Релятивистское дифференциальное уравнение второго порядка для волновой функции частицы со спином 0 … Политехнический терминологический толковый словарь
ВОЛНОВОЕ УРАВНЕНИЕ — в механике, линейное однородное дифф. ур ние в частных производных, описывающее распространение волн в среде; имеет вид: где t время, х, у, z пространственные декартовы координаты, W= W(х, у, z, t) ф ция, характеризующая возмущение среды в точке… … Физическая энциклопедия
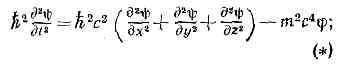 ему соответствует релятив. соотношение между энергией ?и импульсом р ч-цы: ?2=p2c3+m2c4 (m — масса ч-цы). Решением ур-ния (*) явл. ф-ция y(х, у, z, t), зависящая только от координат (х, у, z) и времени (t). Следовательно, ч-цы, состояние к-рых описывается этой ф-цией, не обладают никакими дополнит. внутр. степенями свободы, т. е. действительно явл. бесспиновыми (к таким ч-цам относятся, напр., p- и К-мезоны).Анализ ур-ния показал, что его решение (y) принципиально отличается по своему физ. смыслу от обычной волн. ф-ции как амплитуды вероятности нахождения ч-цы в заданном месте пр-ва в заданный момент времени: y(х, у, z, t) не определяется однозначно значением y в нач. момент времени (такая однозначная зависимость постулируется в квант. механике), и, более того, выражение вероятности состояния наряду с положит. значениями может принимать также и лишённые физ. смысла отрицат. значения. Поэтому сначала от К.— Г.— Ф. у. отказались. Однако в 1934 швейц. физик В. Паули и амер. физик В. Ф. Вайскопф нашли правильную интерпретацию этого ур-ния в рамках квантовой теории поля (они рассмотрели его как ур-ние поля, аналогичное ур-ниям Максвелла для эл.-магн. поля, и проквантовали; при этом y стало оператором).
ему соответствует релятив. соотношение между энергией ?и импульсом р ч-цы: ?2=p2c3+m2c4 (m — масса ч-цы). Решением ур-ния (*) явл. ф-ция y(х, у, z, t), зависящая только от координат (х, у, z) и времени (t). Следовательно, ч-цы, состояние к-рых описывается этой ф-цией, не обладают никакими дополнит. внутр. степенями свободы, т. е. действительно явл. бесспиновыми (к таким ч-цам относятся, напр., p- и К-мезоны).Анализ ур-ния показал, что его решение (y) принципиально отличается по своему физ. смыслу от обычной волн. ф-ции как амплитуды вероятности нахождения ч-цы в заданном месте пр-ва в заданный момент времени: y(х, у, z, t) не определяется однозначно значением y в нач. момент времени (такая однозначная зависимость постулируется в квант. механике), и, более того, выражение вероятности состояния наряду с положит. значениями может принимать также и лишённые физ. смысла отрицат. значения. Поэтому сначала от К.— Г.— Ф. у. отказались. Однако в 1934 швейц. физик В. Паули и амер. физик В. Ф. Вайскопф нашли правильную интерпретацию этого ур-ния в рамках квантовой теории поля (они рассмотрели его как ур-ние поля, аналогичное ур-ниям Максвелла для эл.-магн. поля, и проквантовали; при этом y стало оператором).