КЛЕЙНА - ГОРДОНА УРАВНЕНИЕ
- КЛЕЙНА - ГОРДОНА УРАВНЕНИЕ
- КЛЕЙНА - ГОРДОНА УРАВНЕНИЕ
-
(Клейна - Гордона - Фока уравнение) - простейшее релятивистски-инвариантное ур-ние, описывающее свободное скалярное (или псевдоскалярное) поле физическое. Впервые получено в 1926 Э. Шрёдингеро. <м (как релятивистское обобщение Шрёдингера уравнения )и независимо О. Клейном (О. Klein), В. А. Фоком и В. Гордоном (W. Gordon). В квантовой теории поля применяется для описания частиц со спином 0. В Минковского пространстве-времени К.-Г. у.- линейное однородное диффе-ренц. ур-ние 2-го порядка: 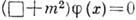 , где
, где  - Д'Аламбера оператор, т - масса частицы,
- Д'Аламбера оператор, т - масса частицы, 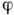 - полевая ф-ция или её компоненты в пространстве внутренней симметрии (х=(х°, х) - точка пространства-времени; используется система единиц, в к-рой
- полевая ф-ция или её компоненты в пространстве внутренней симметрии (х=(х°, х) - точка пространства-времени; используется система единиц, в к-рой 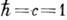 ). Решение К.-Г. у. записывают в виде разложения по плоским волнам:
). Решение К.-Г. у. записывают в виде разложения по плоским волнам:
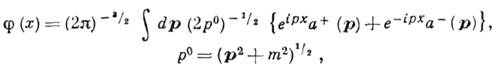
где р = ( р°, р) -4-импульс, px=p°xo-px, а + (р )и а - (р) - положительно- и отрицательно-частотные компоненты Фурье. При каноническом квантовании а + и а - интерпретируются как операторы рождения и уничтожения частицы с импульсом р и энергией р°. В их терминах гамильтониан свободного поля имеет вид .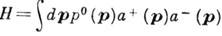 . К.-Г. у. удовлетворяют компоненты любого свободного поля (спинорного, векторного и др.). При m=0 К.-Г. у. переходит в Д'Аламбера уравнение. В римановом пространстве с метрикой
. К.-Г. у. удовлетворяют компоненты любого свободного поля (спинорного, векторного и др.). При m=0 К.-Г. у. переходит в Д'Аламбера уравнение. В римановом пространстве с метрикой 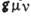 (напр., в присутствии гравитац. поля с такой метрикой) К.-Г. у. имеет вид
(напр., в присутствии гравитац. поля с такой метрикой) К.-Г. у. имеет вид
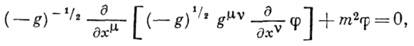
где 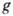 - определитель матрицы
- определитель матрицы 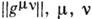 =0, 1, 2, 3.
=0, 1, 2, 3.
Изучены К.-Г. у. с разл. видами нелинейности (напр., синус-Гордона уравнение).
Лит.: Боголюбов Н. Н., Ш и р к о в Д. В., Квантовые поля, М., 1980. В. П. Павлов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1988.
.
Полезное
Смотреть что такое "КЛЕЙНА - ГОРДОНА УРАВНЕНИЕ" в других словарях:
КЛЕЙНА - ГОРДОНА УРАВНЕНИЕ — релятивистски инвариантное квантовое уравнение, описывающее бесспиновые скалярные или псевдоскалярные частицы, напр, p , К мезоны. Уравнение установлено О. Клейном [1] и несколько позднее В. А. Фоком как волновое уравнение при условии цикличности … Математическая энциклопедия
Клейна - Гордона уравнение — квантовое релятивистское (т. е. удовлетворяющее требованиям относительности теории (См. Относительности теория)) уравнение для частиц со спином нуль. Исторически К. Г. у. было первым релятивистским уравнением квантовой механики (См.… … Большая советская энциклопедия
Уравнение Клейна — Гордона — Уравнение Клейна Гордона (Уравнение Клейна Гордона Фока): или, кратко, используя вдобавок естественные единицы (где ): где … Википедия
Уравнение Клейна-Гордона — Уравнение Клейна Гордона (Уравнение Клейна Гордона Фока): или, кратко, используя вдобавок естественные единицы (где ): где оператор Д’Аламбера. является релятивистской версией … Википедия
Уравнение Клейна-Гордона-Фока — Уравнение Клейна Гордона (Уравнение Клейна Гордона Фока): или, кратко, используя вдобавок естественные единицы (где ): где оператор Д’Аламбера. является релятивистской версией … Википедия
Уравнение Клейна — Гордона — Фока — Уравнение Клейна Гордона (Уравнение Клейна Гордона Фока): или, кратко, используя вдобавок естественные единицы (где ): где оператор Д’Аламбера. является релятивистской версией … Википедия
КЛЕЙНА — ГОРДОНА — ФОКА УРАВНЕНИЕ — квантовое релятив. ур ние для ч ц с нулевым спином. Исторически К. Г. Ф. у. явл. первым релятив. ур нием квант. механики для волн. ф ции ч цы (y); оно было предложено в 1926 австр. физиком Э. Шредингером (как релятив. обобщение Шредингера… … Физическая энциклопедия
СИНУС-ГОРДОНА УРАВНЕНИЕ — релятивистски инвариантное ур ние … Физическая энциклопедия
СИНУС ГОРДОНА УРАВНЕНИЕ — Sinе Gоrdоn уравнение, релятивистски инвариантное уравнение, в пространственно временных переменных имеющее вид (A) Название предложено М. Крускалом по аналогии с линейным Клейна Гордона уравнением (где вместо sin истоит и). В характеристических… … Математическая энциклопедия
уравнение клейна-гордона-фока — Релятивистское дифференциальное уравнение второго порядка для волновой функции частицы со спином 0 … Политехнический терминологический толковый словарь
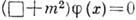 , где
, где  - Д'Аламбера оператор, т - масса частицы,
- Д'Аламбера оператор, т - масса частицы, 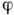 - полевая ф-ция или её компоненты в пространстве внутренней симметрии (х=(х°, х) - точка пространства-времени; используется система единиц, в к-рой
- полевая ф-ция или её компоненты в пространстве внутренней симметрии (х=(х°, х) - точка пространства-времени; используется система единиц, в к-рой 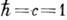 ). Решение К.-Г. у. записывают в виде разложения по плоским волнам:
). Решение К.-Г. у. записывают в виде разложения по плоским волнам: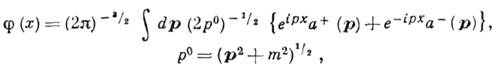
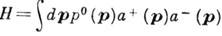 . К.-Г. у. удовлетворяют компоненты любого свободного поля (спинорного, векторного и др.). При m=0 К.-Г. у. переходит в Д'Аламбера уравнение. В римановом пространстве с метрикой
. К.-Г. у. удовлетворяют компоненты любого свободного поля (спинорного, векторного и др.). При m=0 К.-Г. у. переходит в Д'Аламбера уравнение. В римановом пространстве с метрикой 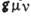 (напр., в присутствии гравитац. поля с такой метрикой) К.-Г. у. имеет вид
(напр., в присутствии гравитац. поля с такой метрикой) К.-Г. у. имеет вид 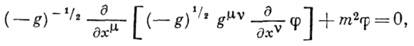
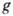 - определитель матрицы
- определитель матрицы 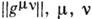 =0, 1, 2, 3.
=0, 1, 2, 3.