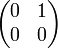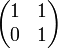Унипотентный элемент

Нильпотентный элемент или нильпотент ― элемент a кольца, удовлетворяющий равенству aⁿ = 0 для некоторого натурального n. Минимальное значение n, для которого справедливо это равенство, называется индексом нильпотентности элемента a.

Рассмотрение нильпотентов часто оказывается полезным в алгебраической геометрии, т. к. они позволяют получить чисто алгебраические аналоги ряда понятий, типичных для анализа и дифференциальной геометрии (бесконечно малые деформации и т. п.).

Примеры

• В кольце вычетов по модулю pⁿ, где p ― некоторое простое число, класс вычетов числа p ― нильпотент индекса n,
• Матрица

$\begin{pmatrix} 0 & 1\\ 0 & 0 \end{pmatrix}$

является нильпотентом индекса 2 в кольце 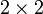$2\times 2$-матриц

Связанные определения

• элемент кольца u называется унипотентным (или унипотентом) если u − 1 является нильпотентным,
  • Например, унипотентной является матрица

    $\begin{pmatrix} 1 & 1\\ 0 & 1 \end{pmatrix}$

Свойства

• Если a ― нильпотентный элемент индекса n, то справедливо равенство

$1=(1-a)(1+a+a^2+\cdots+a^{n-1})$,

т. е. элемент (1 − a) обратим и обратный к нему элемент записывается в виде многочлена от a.

• В коммутативном кольце элемент а нильпотентен тогда и только тогда, когда он содержится во всех простых идеалах.
• Все нильпотентные элементы образуют идеал J, называемым нильрадикалом кольца совпадающий с пересечением всех простых идеалов. Кольцо A / J уже не имеет нильпотентных элементов, отличных от нуля.
• При интерпретации коммутативного кольца как кольца функций на пространстве его спектре нильпотентам соответствуют функции, тождественно равные нулю.