Репер Френе

Репер или трёхгранник Френе или Френе — Серре известный также, как естественный, сопровождающий, сопутствующий — ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых.

Определение

Пусть γ(s) — произвольная натурально параметризованная бирегулярная кривая в евклидовом пространстве. Под репером Френе понимают тройку векторов $\vec{\tau}, \vec{\nu}, \vec{\beta},$ сопоставленную каждой точке бирегулярной кривой $\mathbf{ \gamma(s)}$, где

• $\vec{\tau} = \dot\gamma (s)$ — единичный касательный вектор,
• $\vec{\nu} = {\ddot\gamma (s)\over{||\ddot\gamma (s)||}}$ — единичный вектор главной нормали,
• $\vec{\beta} = \left[ \vec{\tau},\; \vec{\nu} \right]$ — единичный вектор бинормали

к кривой в данной точке.

Формулы Френе

Если s — натуральный параметр вдоль кривой, то векторы $\vec{\tau}, \vec{\nu}, \vec{b}$ связаны соотношениями:

$\dot\vec{\tau} = k \vec{\nu}, \quad \dot\vec{\nu} = - k \vec{\tau} + \kappa \vec{\beta}, \quad \dot\vec{\beta} = - \kappa \vec{\nu},$

называемыми формулами Френе. Величины $k = ||\ddot\gamma (s)||, \quad \kappa = - \langle \dot\vec{\beta},\; \vec{\nu} \rangle$ называют, соответственно, кривизной и кручением кривой в данной точке. Уравнения вида $k = f(s), \quad \kappa = g(s),$ где f(s) всюду положительна называются натуральными уравнениями бирегулярной кривой и полностью её определяют.

Скорость и ускорение в осях естественного трёхгранника

Трёхгранник Френе играет важную роль в кинематике точки при описании её движения в «сопутствующих осях». Пусть материальная точка движется по произвольной бирегулярной кривой. Тогда, очевидно, скорость точки направлена по касательному вектору $\vec{v} = v \vec{\tau}$. Дифференцируя по времени находим выражение для ускорения: $\vec{a} = \dot{v} \vec{\tau} + v^2 k \vec{\nu}$. Компоненту при векторе $\vec{\tau}$ называют тангенциальным ускорением, она характеризует изменение модуля скорости точки. 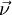Компоненту при векторе $\vec{\nu}$ называют нормальным ускорением. Она показывает, как меняется траектория движения точки.

Вариации и обобщения

При описании плоских кривых часто вводят понятие так называемой ориентированной кривизны.

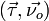Пусть γ(s) - произвольная натурально параметризованная плоская регулярная кривая. Рассмотрим семейство единичных нормалей $\vec{\nu _o}$, таких что двойка $(\vec{\tau},\vec{\nu _o})$ образуют правый базис в каждой точке $\mathbf \gamma(s)$. Ориентированной кривизной кривой γ в точке s называют число $k _o = \langle \ddot\gamma (s),\; \vec{\nu _o} \rangle$. В сделанных предположениях имеет место следующая система уравнений, называемая формулами Френе для ориентированной кривизны

$\dot\vec{\tau} = k _o \vec{\nu _o} \quad \dot\vec{\nu _o} = -k _o \vec{\tau}$.

По аналогии с трёхмерным случаем, уравнения вида k_o = f(s) называются натуральными уравнениями плоской регулярной кривой и полностью её определяют.