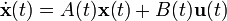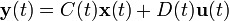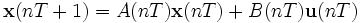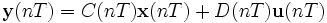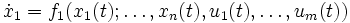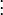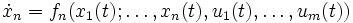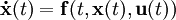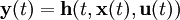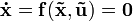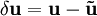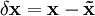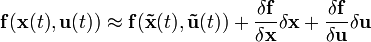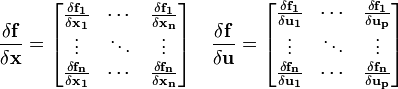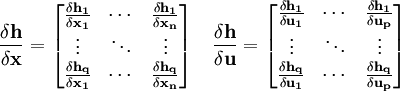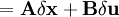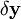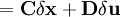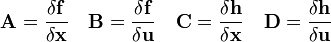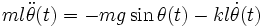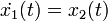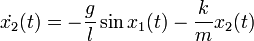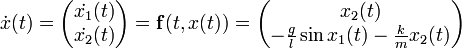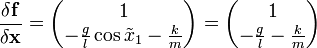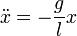- Пространство состояний
-
Пространство состояний — в теории управления один из основных методов описания поведения динамической системы. Движение системы в пространстве состояний отражает изменение его состояний.
Содержание
Определение
В пространстве состояний создаётся модель динамической системы, включающая набор переменных входа, выхода и состояния, связанных между собой дифференциальными уравнениями первого порядка, которые записываются в матричной форме. В отличие от описания в виде передаточной функции и других методов частотной области, пространство состояний позволяет работать не только с линейными системами и нулевыми начальными условиями. Кроме того, в пространстве состояний относительно просто работать с
Линейные непрерывные системы
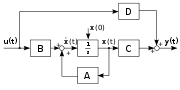 Структурная схема непрерывной линейной системы, описанной в виде переменных состояния
Структурная схема непрерывной линейной системы, описанной в виде переменных состоянияДля случая линейной системы с
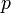 входами,
входами, 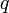 выходами и n переменными состояния описание имеет вид:
выходами и n переменными состояния описание имеет вид:где
 ;
; 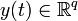 ;
;  ;
;![\operatorname{dim}[A(\cdot)] = n \times n](/pictures/wiki/files/100/d67f69962a6411d08f1ba642d8c75617.png) ,
, ![\operatorname{dim}[B(\cdot)] = n \times p](/pictures/wiki/files/97/a4d9e024860226d6ad283d1d217f1c31.png) ,
, ![\operatorname{dim}[C(\cdot)] = q \times n](/pictures/wiki/files/52/452963fb0f31641c763dab57d77f6d15.png) ,
, ![\operatorname{dim}[D(\cdot)] = q \times p](/pictures/wiki/files/53/5b6e715515525947881d6fb6ea56fb15.png) ,
, 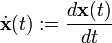 .
.
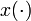 — вектор состояния, элементы которого называются состояниями системы
— вектор состояния, элементы которого называются состояниями системы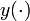 — вектор выхода,
— вектор выхода,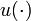 — вектор управления,
— вектор управления, — матрица системы,
— матрица системы,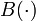 — матрица управления,
— матрица управления,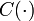 — матрица выхода и
— матрица выхода и — матрица прямой связи.
— матрица прямой связи.
Часто матрица
 является нулевой, это означает, что в системе нет явной прямой связи.
является нулевой, это означает, что в системе нет явной прямой связи.Дискретные системы
Для дискретных систем запись уравнений в пространстве состояний основывается не на дифференциальных, а на разностных уравнениях.
Нелинейные системы
Нелинейная динамическая система n-го порядка может быть описана в виде системы из n уравнений 1-го порядка:
или в более компактной форме:
Первое уравнение — это уравнение состояния, второе — уравнение выхода.
Линеаризация
В некоторых случаях возможна линеаризация описания динамической системы для окрестности рабочей точки
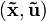 .
.В установившемся режиме
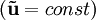 для рабочей точки
для рабочей точки 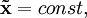 справедливо следующее выражение:
справедливо следующее выражение:Вводя обозначения:
Разложение уравнения состояния
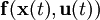 в ряд Тейлора, ограниченное первыми двумя членами даёт следующее выражение:
в ряд Тейлора, ограниченное первыми двумя членами даёт следующее выражение:При взятии частных производных вектор-функции
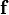 по вектору переменных состояний
по вектору переменных состояний 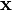 и вектору входных воздействий
и вектору входных воздействий 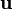 получаются матрицы Якоби соответствующих систем функций:
получаются матрицы Якоби соответствующих систем функций:Аналогично для функции выхода:
Учитывая
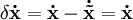 , линеаризованное описание динамической системы в окрестности рабочей точки примет вид:
, линеаризованное описание динамической системы в окрестности рабочей точки примет вид:где
Примеры
Модель в пространстве состояний для маятника
Маятник является классической свободной нелинейной системой. Математически движение маятника описывается следующим соотношением:
где
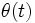 — угол отклонения маятника.
— угол отклонения маятника.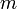 — приведённая масса мaятника
— приведённая масса мaятника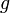 — ускорение свободного падения
— ускорение свободного падения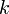 — коэффициент трения в подшипнике подвеса
— коэффициент трения в подшипнике подвеса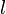 — длина подвеса маятника
— длина подвеса маятника
В таком случае уравнения в пространстве состояний будут иметь вид:
где
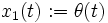 — угол отклонения маятника
— угол отклонения маятника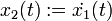 — угловая скорость маятника
— угловая скорость маятника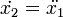 — угловое ускорение маятника
— угловое ускорение маятника
Запись уравнений состояния в общем виде:
Линеаризация модели маятника
Линеаризованная матрица системы для модели маятника в окресности точки равновесия
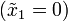 имеет вид:
имеет вид:При отсутствии трения в подвесе
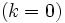 ) получим уравнение движения математического маятника:
) получим уравнение движения математического маятника:См. также
- Теория управления
- Фазовое пространство
- Критерий устойчивости в пространстве состояний
Ссылки
Wikimedia Foundation. 2010.