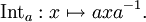- Присоединённая группа
-
Присоединённое представление группы Ли G — линейное представление
 группы G в касательном пространстве TeG (или в алгебре Ли
группы G в касательном пространстве TeG (или в алгебре Ли  группы G), сопоставляющее каждому элементу
группы G), сопоставляющее каждому элементу 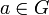 дифференциал
дифференциалЕсли
 — линейная группа в пространстве V, то
— линейная группа в пространстве V, тоДифференциалом присоединённого представления группы G в единице служит присоединённое представление её алгебры Ли.
Связанные определения
- Образом группы Ли G при присоединённом представлении называется присоединённая группа группы G и обозначается
 .
.
Свойства
- Ядро
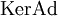 содержит центр группы G.
содержит центр группы G.
- Более того, в случае, когда G связна и основное поле имеет характеристику 0, совпадает с центром.
- Связная полупростая группа Ли изоморфна своей присоединённой группе тогда и только тогда, когда её корни порождают группу рациональных характеров максимального тора; центр такой группы тривиален.
- Если основное поле имеет характеристику 0 и G связна, то
 однозначно определяется алгеброй Ли
однозначно определяется алгеброй Ли  и называется иногда присоединённой группой, или группой внутренних автоморфизмов, алгебры Ли
и называется иногда присоединённой группой, или группой внутренних автоморфизмов, алгебры Ли  .
.
- В частности, если G полупроста, то
 совпадает со связной компонентой единицы в
совпадает со связной компонентой единицы в 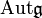 .
.
- В частности, если G полупроста, то
Wikimedia Foundation. 2010.