Приводимое представление

Представле́ние гру́ппы, точнее линейное представление группы — гомоморфизм заданной группы в группу невырожденных линейных преобразований векторного пространства. Образ этого гомоморфизма сам является группой, элементами которой являются соответствующие линейные преобразования или их матрицы. То есть, представление группы, G, есть гомоморфизм групп

$h:G\to\operatorname{Aut}(W)$,

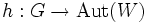где 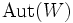$\operatorname{Aut}(W)$ обозначает группу автоморфизмов векторного пространства W.

Представление можно понимать как запись группы с помощью матриц или преобразований линейного пространства. Например, унитарная группа U(1) может быть представлена как группа из вращений двухмерного пространства вокруг центра. Смысл использования представлений групп заключается в том, что задачи из теории групп сводятся к более наглядным задачам из линейной алгебры.

Раздел математики, который изучает представления групп, называется теорией представлений групп.

Типы представлений

• Представление группы в пространстве которого есть собственное инвариантное подпространство называется приводимым; в противном случае — неприводимым или простым.
• Если G ― топологическая группа, то под представлением G обычно понимается непрерывное линейное представление группы G в топологическом векторном пространстве.

Вариации и обобщения

В более широком смысле, под представлением группы может пониматься гомоморфизм группы в группу всех обратимых преобразований некоторого множества X. Например:

• Проективное представление группы — гомоморфизм группы в группу проективных преобразований проективного пространства.