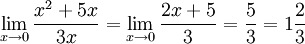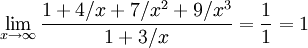- Правило Лопиталя - Бернулли
-
В математическом анализе правилом Лопита́ля называют метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и
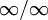 . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.Содержание
Точная формулировка
Правило говорит, что если функции f(x) и g(x) обладают следующим набором условий:
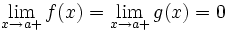 или
или 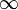 ;
;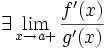 ;
;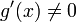 в проколотой окрестности a;
в проколотой окрестности a;- Если g(x) и f(x) — дифференцируемы в проколотой окрестности a,
тогда существует
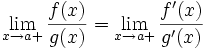 . При этом теорема верна и для других баз (для указанной будет приведено доказательство).
. При этом теорема верна и для других баз (для указанной будет приведено доказательство).История
Способ раскрытия такого рода неопределённостей был опубликован Лопиталем в его сочинении «Анализ бесконечно малых», изданном в 1696 году. В предисловии к этому сочинению Лопиталь указывает, что без всякого стеснения пользовался открытиями Лейбница и братьев Бернулли и «не имеет ничего против того, чтобы они предъявили свои авторские права на все, что им угодно». Иоганн Бернулли предъявил претензии на все сочинение Лопиталя целиком и в частности после смерти Лопиталя опубликовал работу под примечательным названием «Усовершенствование моего опубликованного в „Анализе бесконечно малых“ метода для определения значения дроби, числитель и знаменатель которой иногда исчезают», 1704.
Доказательство
Отношение бесконечно малых
Докажем теорему для случая, когда пределы функций равны нулю (т. н. неопределённость вида
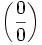 ).
).Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a, мы можем непрерывным образом их доопределить в этой точке: пусть f(a) = g(a) = 0. Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку
![[a,\;x]](/pictures/wiki/files/102/f129b8fafa10306d22163927df18c5d0.png) теорему Коши. По этой теореме получим:
теорему Коши. По этой теореме получим:![\exists c \in [a,x]\!:\frac{f(x)-f(a)}{g(x)-g(a)}=\frac{f'(c)}{g'(c)}](/pictures/wiki/files/57/9ca452ab9c181d7cc25cfee718cbd4f9.png) ,
,
но f(a) = g(a) = 0, поэтому
![\forall x\, \exists c \in [a,\;x]\!:\frac{f(x)}{g(x)}=\frac{f'(c)}{g'(c)}](/pictures/wiki/files/56/88658f13683a2524b05d1c02b309fd8d.png) .
.Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим:
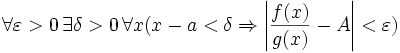 для конечного предела и
для конечного предела и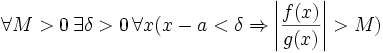 для бесконечного,
для бесконечного,
что является определением предела отношения функций.
Отношение бесконечно больших
Докажем теорему для неопределённостей вида
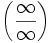 .
.Пусть, для начала, предел отношения производных конечен и равен A. Тогда, при стремлении x к a справа, это отношение можно записать как A + α, где α — O(1). Запишем это условие:
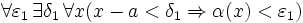 .
.
Зафиксируем t из отрезка
![[a,\;a+\delta_1]](/pictures/wiki/files/54/61868fac131522007230e1cdf0a70e53.png) и применим теорему Коши ко всем x из отрезка
и применим теорему Коши ко всем x из отрезка ![[a,\;t]](/pictures/wiki/files/52/481aea3c1b6b4518052606d8cfd075ba.png) :
:![\forall x\in [a;t]\ \exists c\in [a;\;x]\!:\frac{f(x)-f(t)}{g(x)-g(t)}=\frac{f'(c)}{g'(c)}](/pictures/wiki/files/49/19c28c333bb20569a0f9c7c0fd2c8a6f.png) , что можно привести к следующему виду:
, что можно привести к следующему виду: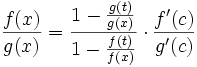 .
.
Для x, достаточно близких к a, выражение имеет смысл; предел первого множителя правой части равен единице (так как f(t) и g(t) — константы, а f(x) и g(x) стремятся к бесконечности). Значит, этот множитель равен 1 + β, где β — бесконечно малая функция при стремлении x к a справа. Выпишем определение этого факта, используя то же значение
 , что и в определении для α:
, что и в определении для α: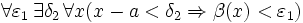 .
.
Получили, что отношение функций представимо в виде (1 + β)(A + α), и
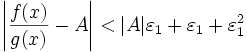 . По любому данному
. По любому данному  можно найти такое
можно найти такое 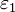 , чтобы модуль разности отношения функций и A был меньше
, чтобы модуль разности отношения функций и A был меньше  , значит, предел отношения функций действительно равен A.
, значит, предел отношения функций действительно равен A.Если же предел A бесконечен (допустим, он равен плюс бесконечности), то
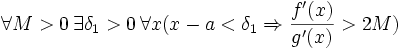 .
.
В определении β будем брать
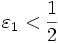 ; первый множитель правой части будет больше 1/2 при x, достаточно близких к a, а тогда
; первый множитель правой части будет больше 1/2 при x, достаточно близких к a, а тогда 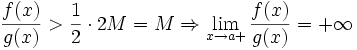 .
.Для других баз доказательства аналогичны приведённым.
Примеры
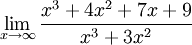
Здесь можно применить правило Лопиталя 3 раза, а можно поступить иначе. Можно разделить и числитель, и знаменатель на x в наибольшей степени(в нашем случае x3). В этом примере получается: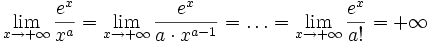 ;
;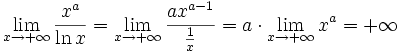 при a > 0.
при a > 0.
(Только если числитель и знаменатель ОБА стремятся или к 0; или к
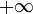 ; или к
; или к 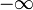 .)
.)
Wikimedia Foundation. 2010.