Полная решетка

Полная решётка — частично упорядоченное множество, в котором всякое непустое подмножество A имеет точную верхнюю и нижнюю грань, называемые обычно объединением и пересечением элементов подмножества A и обозначаемые 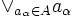$\vee_{a_{\alpha} \in A} a_{\alpha}$ и $\land_{a_{\alpha} \in A} a_{\alpha}$ (или просто $\vee A$ и $\land A$) соответственно. Относительно операций объединения и пересечения полная решётка является решёткой.

Свойства

• Решётка L тогда и только тогда является полной, когда для любого изотонного отображения φ этой решётки в себя существует неподвижная точка, то есть такой элемент 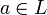$a \in L$, что aφ = a.
• Всякое частично упорядоченное множество P можно изоморфно вложить в полную решётку, которая в этом случае называется пополнением множества множества P. Пополнение сечениями является наименьшим из всех пополнений данного частично упорядоченного множества.

Примеры

• множество всех подалгебр универсальной алгебры;
• множество всех конгруэнций универсальной алгебры;
• множество всех замкнутых подмножеств топологического пространства.
• Если частично упорядоченное множество имеет наибольший элемент и каждое его непустое подмножество обладает точной нижней гранью, то оно является полной решёткой.
• Если P(M) — упорядоченное включением множество подмножеств множества M и φ — отношение замыкания на P(M), то совокупность всех φ-замкнутых подмножеств является полной решёткой.

Литература

• Биркгоф Г. Теория структур. — пер. с англ., М., 1952.
• Скорняков Л. А. Элементы теории структур. — М., 1970.
• Математическая энциклопедия

См. также

• Решётка