- РЕГУЛЯРНАЯ РЕШЕТКА
структура ре гулярная,- условно полная решетка (структура), в к-рой выполняется следующее условие (наз. также а к с и о м о й р е г у л я р н о с т и): для любой последовательности { Е п}ограниченных множеств, для к-рой
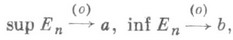 найдутся конечные подмножества
найдутся конечные подмножества  с тем же свойством
с тем же свойством 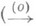 означает сходимость по упорядочению). Такие структуры (в первую очередь регулярные K- пространства и булевы алгебры) чаще всего встречаются в функциональном анализе и теории меры. Они естественно возникают в задаче продолжения гомоморфизмов и линейных положительных операций. В Р. р. выполняются следующие два принципа: а) принцип диагонали (если
означает сходимость по упорядочению). Такие структуры (в первую очередь регулярные K- пространства и булевы алгебры) чаще всего встречаются в функциональном анализе и теории меры. Они естественно возникают в задаче продолжения гомоморфизмов и линейных положительных операций. В Р. р. выполняются следующие два принципа: а) принцип диагонали (если 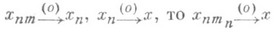 для нек-рой последовательности индексов т п )и б) принцип счетности типа (всякое бесконечное ограниченное множество содержит счетную часть с теми же гранями). В свою очередь, а) и б) вместе эквивалентны аксиоме регулярности. Примеры Р. р.: всякое KВ -пространство и, в частности, всякое
для нек-рой последовательности индексов т п )и б) принцип счетности типа (всякое бесконечное ограниченное множество содержит счетную часть с теми же гранями). В свою очередь, а) и б) вместе эквивалентны аксиоме регулярности. Примеры Р. р.: всякое KВ -пространство и, в частности, всякое 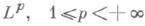 ; булева алгебра mod 0 измеримых множеств произвольного пространства с конечной счетно аддитивной мерой. Другие известные примеры регулярных булевых алгебр основываются на отрицании Суслина гипотезы.
; булева алгебра mod 0 измеримых множеств произвольного пространства с конечной счетно аддитивной мерой. Другие известные примеры регулярных булевых алгебр основываются на отрицании Суслина гипотезы.
Лит.:[1] К а н т о р о в и ч Л. В., В у л и х Б. З., П и н с к е р А. Г., Функциональный анализ в полуупорядоченных пространствах, М.- Л., 1950. Д. А. Владимиров.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
