Плюс Клини

Звезда́ Кли́ни (или замыка́ние Кли́ни) в математической логике и информатике — унарная операция над множеством строк либо символов. Замыкание Клини множества V обозначается V*. Широко применяется в регулярных выражениях, на примере которых было введено Стивеном Клини для описания некоторых автоматов.

Если V — множество строк

то V* — минимальное надмножество множества V, которое содержит ε (пустую строку (англ.)) и замкнуто относительно конкатенации. Это также множество всех строк, полученных конкатенацией нуля или более строк из V.

Если V — множество символов

то V* — множество всех строк из символов из V с добавлением пустой строки.

Определение

Степень множества

Нулевая степень любого множества неизменна:

$V^0 = \left\{\epsilon \right\}$.

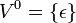Остальные степени определяются рекурсивно:

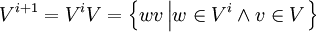$V^{i+1} = V^i V = \left\{wv \left| w \in V^i \land v \in V \right.\right\}$, где $i \in \N_0$.

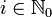Если V — множество символов

то Vⁱ — множество строк длиной i символов, взятых из V.

Звезда Клини

Замыкание Клини множества V есть

$V^* = \bigcup_{i=0}^{\infty} V^i$.

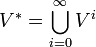То есть это множество всех строк конечной длины́, порождённое элементами множества V.

Плюс Клини

Есть операция, аналогичная звезде Клини, — плюс Клини:

$V^+ = \bigcup_{i=1}^{\infty} V^i$.

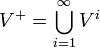Как видим, отличается тем, что пропущено V⁰, содержащее пустую строку.

Свойства

• Связь операций:
  1. V ⁺ = V ^* V
  2. $V^+ = V^* \Leftrightarrow \epsilon \in V$
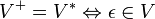
• Идемпотентность:

$V^* = {V^*}^*$.

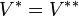• Замыкание Клини включает в себя порождающее множество:

$V \subseteq V^*$.

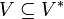• Замыкание Клини всегда содержит пустую строку:

$\epsilon \in V^*$.

• Счётность:

$\left|V^* \right| = \left|V^+ \right| = \alef_0 \Leftarrow \varnothing \not= V \not= \left\{\epsilon \right\}$.

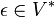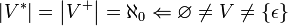Примеры

Для множества строк

{"Go", "Russia"}* = {ε, "Go", "Russia", "GoGo", "GoRussia", "RussiaGo", "RussiaRussia", "GoGoGo", "GoGoRussia", "GoRussiaGo", …}.

Для множества символов

{'a', 'b', 'c'}* = {ε, "a", "b", "c", "aa", "ab", "ac", "ba", "bb", "bc", "ca", "cb", "cc", "aaa", …}.

Для множества из пустой строки

$\left\{\epsilon \right\}^* = \left\{\epsilon \right\}^+ = \left\{\epsilon \right\}$.

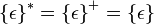Для пустого множества

$\varnothing^* = \left\{\epsilon \right\}$.

$\varnothing^+ = \varnothing^* \varnothing = \varnothing$.

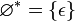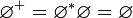Обобщение

Стро́ки образуют моноид по конкатенации с нейтральным элементом ε. Таким образом, определение звезды́ Клини можно распространить на любой моноид.

Литература

• John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman. Introduction to Automata Theory, Languages, and Computation. — 3rd Edition. — 2006. — 535 p. — ISBN 0321462254
• Katrin Erk, Lutz Priese. Theoretische Informatik: eine umfassende Einführung. — 2., erw. — Springer-Verlag, 2002. — С. 27—29. — ISBN 3-540-42624-8

См. также

• Алгебра Клини
• Регулярные выражения
• Расширенная Бэкус — Наурова форма
• Лемма о разрастании