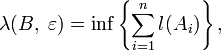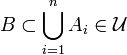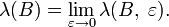Плоская печать — в полиграфии способ печати, использующий формы, на которых печатающие и пробельные элементы расположены в одной плоскости и различаются лишь физико химическими свойствами. Основой для форм плоской печати, как правило, служат металлические… … Википедия
Вариация отображения — Вариация отображения числовая характеристика отображения, связанная с его дифференциальными свойствами. Понятие «вариация отображения» было определено С. Банахом[1]. Двухмерный случай Рассмотрим определение вариации отображения для… … Википедия
Соединённые Штаты Америки — Соединенные Штаты Америки США, гос во в Сев. Америке. Название включает: геогр. термин штаты (от англ, state государство ), так в ряде стран называют самоуправляющиеся территориальные единицы; определение соединенные, т. е. входящие в федерацию,… … Географическая энциклопедия
Франция* — (France, Frankreich). Расположение, границы, пространство. С севера Ф. омывает Немецкое море и Ла Манш, с запада Атлантический океан, с юго востока Средиземное море; на северо востоке она граничит с Бельгией, Люксембургом и Германией, на востоке… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Франция — I (France, Frankreich). Расположение, границы, пространство. С севера Ф. омывает Немецкое море и Ла Манш, с запада Атлантический океан, с юго востока Средиземное море; на северо востоке она граничит с Бельгией, Люксембургом и Германией, на… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
АР — (егип.). Коза. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АР (франц. are, от лат. area плоская поверхность). Французская мера поверхности = 100 кв. метрам, около 22 кв. саженей. Словарь иностранных слов,… … Словарь иностранных слов русского языка
Германия — I союз государств или союзное государство [Мы не останавливаемся решительно ни на одном из этих терминов (Staatenbund. Bundesstaat), потому что Герм. империя, как будет объяснено ниже не подходит вполне ни под тот, ни под другой] в средней Европе … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
КООРДИНАЦИОННОЕ ЧИСЛО — число ближайших к данному атому соседних атомов в кристаллической решётке (атомной структуре кристалла) или молекул в молекулярных кристаллах. Если центры этих ближайших соседей соединить друг с другом прямыми линиями, то получится плоская фигура … Физическая энциклопедия
Капуста — (Brassica L.). Род растений из сем. крестоцветных (см.). Однолетние, двулетние и многолетние травы с перисто раздельными или лопастными листьями. Чашелистики растопыренные или приподнятые горизонтально; лепестки желтые или белые, иногда с… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ОБУВЬ — служит для защиты ног (ступни и голени) от механических повреждении, про мачивания и охлаждения. Гигиенические требования, предъявляемые к О. заключаются в том, что: 1) О. не должна препятствовать естественному развитию стопы и должна… … Большая медицинская энциклопедия
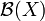 метрического пространства X.
метрического пространства X.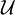 открытых подмножеств X, на котором определил неотрицательную функцию
открытых подмножеств X, на котором определил неотрицательную функцию 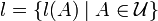 и
и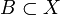 множествами из
множествами из 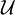 с диаметром, не превосходящим
с диаметром, не превосходящим  , то есть
, то есть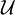 и функцией l, называется предел
и функцией l, называется предел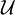 — совокупность всех шаров в X, a
— совокупность всех шаров в X, a 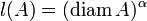 , где α > 0. Тогда соответствующая мера λ будет называться α-мерой Хаусдорфа. При α = 1 такая мера будет называться линейной мерой Хаусдорфа, а при α = 2 — плоской мерой Хаусдорфа.
, где α > 0. Тогда соответствующая мера λ будет называться α-мерой Хаусдорфа. При α = 1 такая мера будет называться линейной мерой Хаусдорфа, а при α = 2 — плоской мерой Хаусдорфа.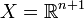 ,
, 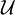 — совокупность цилиндров с шаровыми основаниями и осями, параллельными направлению оси xn + 1 и l(A) равна n-мерному объёму осевого сечения цилиндра
— совокупность цилиндров с шаровыми основаниями и осями, параллельными направлению оси xn + 1 и l(A) равна n-мерному объёму осевого сечения цилиндра 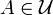 , то соответствующая мера Хаусдорфа называется цилиндрической мерой.
, то соответствующая мера Хаусдорфа называется цилиндрической мерой.