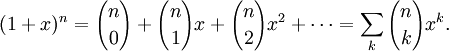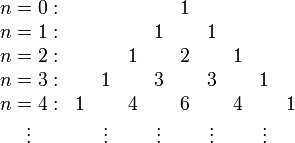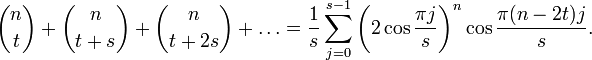- Паскаля треугольник
-
Биномиальные коэффициенты — коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона):
Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов.
Значение биномиального коэффициента
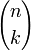 определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов:
определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов: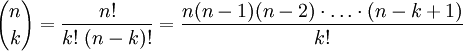 для
для 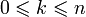 ;
;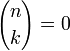 для k < 0 или
для k < 0 или 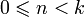 ;
;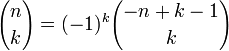 для
для 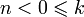 ,
,
где n! и k! — факториалы чисел n и k.
Биномиальный коэффициент
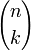 является обобщением числа сочетаний
является обобщением числа сочетаний 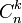 , которое определено только для неотрицательных целых чисел n, k.
, которое определено только для неотрицательных целых чисел n, k.Биномиальные коэффициенты часто возникают в комбинаторных задачах и теории вероятностей.
Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.
Содержание
Треугольник Паскаля

Тождество
позволяет расположить биномиальные коэффициенты для неотрицательных n, k в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих:
Треугольная таблица, предложенная Паскалем в «Трактате об арифметическом треугольнике» (1654), отличается от выписанной здесь поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье, О. Хайяму и др.).
Свойства
Интересно, что если рассмотреть ряды в треугольнике Паскаля, состоящие из биномиальных коэффициентов, то в пределе получим функцию нормального распределения — распределение Гаусса.
Из теоремы Люка следует, что:
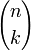 нечётен
нечётен 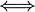 в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули,
в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули,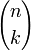 некратен простому p
некратен простому p 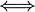 в p-ичной записи числа k все разряды не превосходят соотв. разрядов числа n,
в p-ичной записи числа k все разряды не превосходят соотв. разрядов числа n,- В ряду биномиальных коэффициентов
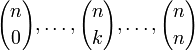 :
:
- все числа не кратны заданному простому p
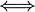 n = mpk − 1, где натуральное m < p,
n = mpk − 1, где натуральное m < p, - все числа, кроме первого и последнего, кратны заданному простому p
 n = pk, где натуральное m < p,
n = pk, где натуральное m < p, - количество нечётных чисел равно степени двойки,
- не может быть поровну чётных и нечётных чисел,
- количество не кратных простому p чисел равно
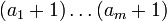 , где числа
, где числа 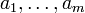 — разряды p-ичной записи числа n; а число m = [logpn] + 1
— разряды p-ичной записи числа n; а число m = [logpn] + 1
- все числа не кратны заданному простому p
Тождества
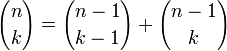
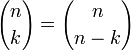 (правило симметрии)
(правило симметрии)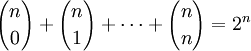
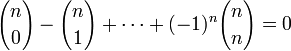
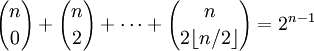
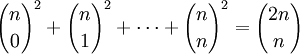
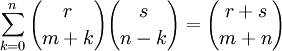 (свёртка Вандермонда)
(свёртка Вандермонда)- Мультисекция ряда (1 + x)n дает следующее тождество, выражающее суммы биномиальных коэффициентов с произвольным шагом s
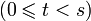 в виде замкнутой суммы из s слагаемых:
в виде замкнутой суммы из s слагаемых:
Асимптотика и оценки
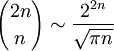
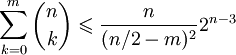 при m < n / 2 (неравенство Чебышёва)
при m < n / 2 (неравенство Чебышёва)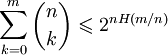 (энтропийная оценка), где H(x) = − xlog2x − (1 − x)log2(1 − x) — энтропия.
(энтропийная оценка), где H(x) = − xlog2x − (1 − x)log2(1 − x) — энтропия.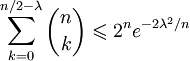 (неравенство Чернова)
(неравенство Чернова)
Алгоритмы вычисления биномиальных коэффициентов
Биномиальные коэффициенты могут быть вычислены с помощью формулы
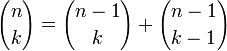 , если на каждом шаге хранить значения
, если на каждом шаге хранить значения 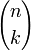 при
при 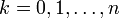 . Этот алгоритм особенно эффективен, если нужно получить все значения
. Этот алгоритм особенно эффективен, если нужно получить все значения 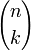 при фиксированном n. Алгоритм требует O(n) памяти (O(n2) при вычислении всей таблицы биномиальных коэффициентов) и O(n2) времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).
при фиксированном n. Алгоритм требует O(n) памяти (O(n2) при вычислении всей таблицы биномиальных коэффициентов) и O(n2) времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).Второй способ основан на тождестве
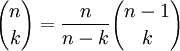 . Он позволяет вычислить значения
. Он позволяет вычислить значения 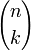 при фиксированном k. Алгоритм требует O(1) памяти (O(l) если нужно посчитать l последовательных коэффициентов с фиксированным k) и O(k) времени.
при фиксированном k. Алгоритм требует O(1) памяти (O(l) если нужно посчитать l последовательных коэффициентов с фиксированным k) и O(k) времени.См. также
- Биномиальное распределение
- Треугольное число
- Треугольник Паскаля
- Пирамида Паскаля
- Композиция (теория чисел)
- Разбиение числа
Ссылки
- О. В. Кузьмин Треугольник и пирамида Паскаля: свойства и обобщения // Соросовский Образовательный Журнал. — 2000. — Т. 6. — № 5. — С. 101—109.
- С. К. Абачиев Радужная фрактальность треугольника Паскаля
Wikimedia Foundation. 2010.