- Треугольное число
-
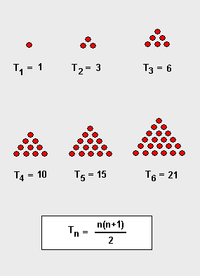
Треугольное число — это число кружков, которые могут быть расставлены в форме равностороннего треугольника, см. рисунок. Очевидно, с чисто арифметической точки зрения, n-е треугольное число — это сумма n первых натуральных чисел.
Последовательность треугольных чисел
 для n = 0, 1, 2, … начинается так:
для n = 0, 1, 2, … начинается так:Содержание
Свойства
- Формулы для n-го треугольного числа:
 ;
; ;
; — биномиальный коэффициент.
— биномиальный коэффициент.
- Сумма двух последовательных треугольных чисел — это квадратное число, то есть
 .
.
- Каждое чётное совершенное число является треугольным.
- Любое число представимо в виде суммы не более трёх треугольных чисел. Утверждение впервые сформулировано в 1638 году Пьером Ферма в письме к Мерсенну, а доказано в 1796 году К. Гауссом.
- Целое число m является треугольным тогда и только тогда, когда число 8m+1 является квадратным.
Исторический анекдот о Гауссе
По широко распространённой[1] легенде школьный учитель Карла Фридриха Гаусса, когда последнему было 10 лет, предложил своим ученикам найти сумму всех натуральных чисел от одного до ста.
Маленький Карл удивил всех, практически мгновенно предложив правильный ответ. Он заметил, что сумма каждой пары слагаемых, одинаково отстоящих от концов ряда натуральных чисел [1..100], равна 101 (1+100, 2+99, 3+98,…, 50+51). А поскольку число таких пар равно 100/2, то есть 50, он посчитал в уме, что искомая сумма равна 101 × 50 = 5050.[2][3]
Обобщения
Треугольные числа являются частным случаем многоугольных чисел.
Примечания
- ↑ Versions of the Gauss Schoolroom Anecdote
- ↑ Идеи гуманитаризации — на каждый урок математики!, 3. Учись учиться. Яковлева Татьяна Петровна, доцент кафедры прикладной математики
- ↑ А. Я. Котов Глава десятая. §1. Знаменитые математики и вычислители // Вечера занимательной арифметики. — Издание 2-е, исправленное и дополненное. — М.: Просвещение, 1967. — С. 131-132. — 184 с. — 150 тыс, экз.
См. также
- Фигурные числа
- Квадратное число
- Треугольное квадратное число
- Тетраэдрические числа
- Треугольник Паскаля
- Пирамида Паскаля
- Задача о числе касаний
 Категория:
Категория:- Фигурные числа
- Формулы для n-го треугольного числа:
Wikimedia Foundation. 2010.