Неравенство Чебышёва

Неравенство Чебышёва

В Википедии существует другое неравенство, носящее имя Чебышёва — см. Неравенство Чебышёва для сумм.

Нера́венство Чебышёва, известное также как неравенство Биенэме — Чебышева, это распространённое неравенство из теории меры и теории вероятностей. Оно было первый раз получено Биенэме (фран.) в 1853 году, и позже также Чебышёвом. Неравенство, использующееся в теории меры, является более общим, в теории вероятностей используется его следствие.

Неравенство Чебышёва в теории меры

Неравенство Чебышёва в теории меры описывает взаимосвязь интеграла Лебега и меры. Аналог этого неравенства в теории вероятностей — неравенство Маркова. Неравенство Чебышёва также используется для доказательства вложения пространства L_p в .

Формулировки

• Пусть 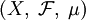$(X,\;\mathcal{F},\;\mu)$ - пространство с мерой.
  И пусть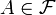
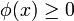  • $A\in\mathcal{F}$
  • $\phi(x)\geq 0$ - суммируемая на A функция
  • c > 0.

Тогда справедливо неравенство:

$\mu\{x:x\in A,\phi(x)\geq c\}\leq\frac{1}{c}\int\limits_A\phi(x)\mu(dx)$.

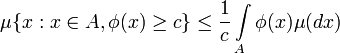• В более общем виде:

Если g - неотрицательная вещественная измеримая функция, неубывающая на области определения φ, то

$\mu(\{x\in A\,:\,\,\phi(x)\geq t\}) \leq {1\over g(t)} \int_A g\circ \phi\, \mu(dx).$

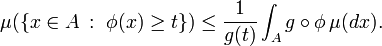
• В терминах пространства L_p:

Пусть $\phi(x)\in L_p$,

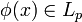тогда $\mu\left\{x\in A\mid |\phi(x)| > t\right\}\le \frac{\|\phi\|_p^p}{t^p}.$

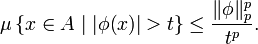
Неравенство Чебышёва в теории вероятностей

Неравенство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего. Неравенство Чебышёва является следствием неравенства Маркова.

Формулировки

Пусть случайная величина 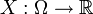$X:\Omega \to \mathbb{R}$ определена на вероятностном пространстве 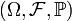$(\Omega, \mathcal{F},\mathbb{P})$, и её математическое ожидание μ и дисперсия σ² конечны. Тогда

$\mathbb{P}\left(|X-\mu|\geqslant a\right) \leqslant \frac{\sigma^2}{a^2}$,

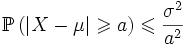где a > 0.

Если a = kσ, где σ — стандартное отклонение и k > 0, то получаем

$\mathbb{P}\left(|X-\mu|\geqslant k \sigma \right) \leqslant \frac{1}{k^2}$.

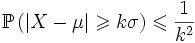В частности, случайная величина с конечной дисперсией отклоняется от среднего больше, чем на 2 стандартных отклонения с вероятностью меньше 25%. Она отклоняется от среднего на 3 стандартных отклонения с вероятностью меньше 11,2%.

См. также

• Неравенство Маркова
• Неравенство Чебышёва для сумм

Литература

• Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. — изд. четвёртое, переработанное. — М.: Наука, 1976. — 544 с.