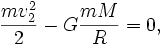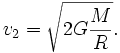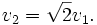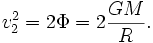Параболическая скорость

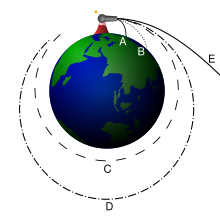Анализ второй космической скорости по Исаку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос.

Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела. Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).

Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для Солнца вторая космическая скорость составляет 617,7 км/с.

Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.

Вывод формулы

Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.

Запишем закон сохранения энергии

$\frac{mv_2^2}{2}-G\frac{mM}{R}=0,$

где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G — гравитационная постоянная, v₂ — вторая космическая скорость.

Разрешая относительно v₂, получим

$v_2=\sqrt{2G\frac{M}{R}}.$

Между первой и второй космическими скоростями существует простое соотношение:

$v_2=\sqrt{2}v_1.$

Квадрат скорости убегания равен удвоенному ньютоновскому потенциалу в данной точке (например, на поверхности планеты):

$v_2^2=2\Phi=2\frac{GM}{R}.$

Вторая космическая скорость (скорость освобождения) на поверхности некоторых небесных тел

Небесное тело	Масса (по отношению к массе Земли	2-я космическая скорость, км/с	Небесное тело	Масса (по отношению к массе Земли	2-я космическая скорость, км/с
Меркурий	0,055	4,3	Сатурн	95,3	36,0
Венера	0,82	10,22	Уран	14,5	22,0
Земля	1	11,2	Нептун	17,5	24,0
Марс	0,108	5,0	Луна	0,0123	2,4
Юпитер	318,3	61,0	Солнце	333 000	617,7
Сириус В	325 675	10 000	Нейтронная звезда	666 000	200 000
Кварковая звезда	832 500	300 000	Чёрная дыра	832 500 - 5,6*1015	Бесконечность

См. также

• Первая космическая скорость
• Третья космическая скорость
• Четвёртая космическая скорость