Окрестностный ретракт

Ретракт топологического пространства X — подпространство A этого пространства, для которого существует ретракция X на A; то есть непрерывное отображение $f:X\to A$, тождественное на A (то есть такое, что f(x) = x при всех $x\in A$).

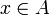Ретракт топологического пространства наследует многие важные свойства самого пространства, в то же время он может быть устроен гораздо проще его самого, более обозрим, более удобен для конкретного исследования.

Примеры

• Одноточечное множество является ретрактом отрезка, прямой, плоскости и т. д.
• Всякое непустое замкнутое множество канторова совершенного множества является его ретрактом.
• n-мерная сфера не является ретрактом (n + 1)-мерного шара евклидова пространства, так как шар имеет нулевые группы гомологий, а сфера — ненулевую группу H_n. Это противоречит существованию ретракта, так как ретракция индуцирует эпиморфизм групп гомологий.

Связанные определения

• Подпространство A пространства X называется окрестностным ретрактом, если в X существует открытое подпространство, содержащее A, ретрактом которого является A.
• Метризуемое пространство X называется абсолютным ретрактом (абсолютным окрестностным ретрактом), если оно является ретрактом (соответственно окрестностным ретрактом) всякого метризуемого пространства, содержащего X в качестве замкнутого подпространства.
• Если ретракция пространства X на его подпространство A гомотопна тождественному отображению пространства X на себя, то A называется деформационным ретрактом пространства X.

Свойства

• Подпространство A пространства X является его ретрактом в том и только в том случае, если всякое непрерывное отображение пространства A в произвольное топологического пространство Y можно продолжить до непрерывного отображения всего пространства X в Y.
• Если пространство X хаусдорфово, то всякий ретракт пространства X замкнут в X.
• Всякое свойство, сохраняющееся при переходе к непрерывному образу, равно как и любое свойство, наследуемое замкнутыми подпространствами, устойчиво относительно перехода к ретракту. В частности, при переходе к ретракту сохраняются
  • компактность,
  • связность,
  • линейная связность,
  • сепарабельность,
  • ограничение сверху на размерность,
  • паракомпактность,
  • нормальность,
  • локальная компактность,
  • локальная связность.
• Если пространство X имеет свойство неподвижной точки, т.е . для каждого непрерывного отображения 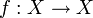$f:X\to X$ существует точка $x\in X$ такая, что f(x) = x, то и каждый ретракт пространства X обладает свойством неподвижной точки.
• Абсолютный окрестностный ретракт является локально стягиваемым пространством.
• Ретракция индуцирует эпиморфизм групп гомологий.

Литература

• Борсук К., Теория ретрактов, пер. с англ., М., 1971.