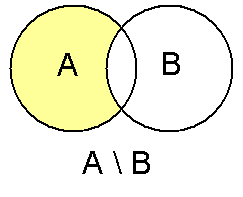
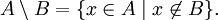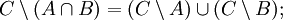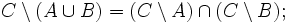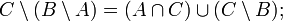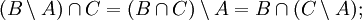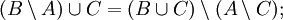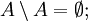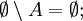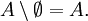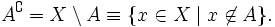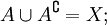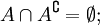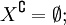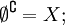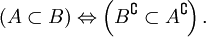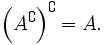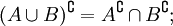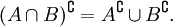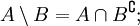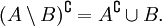Несимметричная разность множеств

Дополне́ние в теории множеств — это семейство элементов, не принадлежащих данному множеству.

Разность множеств

Определение

Пусть даны два множества A и B. Тогда их (теоретико-множественная) разность определяется следующим образом:

$A \setminus B = \{ x\in A \mid x \not\in B \}.$

Примеры

• Пусть 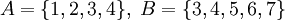$A = \{1,2,3,4\},\; B = \{3,4,5,6,7\}$. Тогда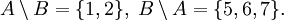 $A \setminus B = \{1,2\},\; B \setminus A = \{5,6,7\}.$
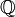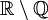• Пусть $\mathbb{R}$ — множество всех вещественных чисел, $\mathbb{Q}$ — множество рациональных чисел, а $\mathbb{Z}$ — множество целых чисел. Тогда $\mathbb{R}\setminus\mathbb{Q}$ — множество всех иррациональных чисел, а 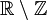$\mathbb{R}\setminus \mathbb{Z}$ — дробных.

Свойства

Пусть A,B,C — произвольные множества. Тогда

• $C \setminus (A \cap B ) = (C \setminus A) \cup (C \setminus B);$
• $C \setminus (A \cup B ) = (C \setminus A) \cap (C \setminus B);$
• $C \setminus( B \setminus A ) = (A \cap C) \cup (C \setminus B);$
• $(B \setminus A) \cap C = (B \cap C) \setminus A = B \cap (C \setminus A);$
• $(B \setminus A) \cup C = (B \cup C) \setminus (A \setminus C);$
• $A \setminus A = \emptyset;$
• $\emptyset \setminus A = \emptyset;$
• $A \setminus \emptyset = A.$

Компьютерные реализации

В пакете функции Complement. В пакете setdiff.

Дополнение множества

Определение

Если из контекста следует, что все рассматриваемые множества являются подмножествами некоторого фиксированного универсального множества X, то определяется операция дополнения:

$A^{\complement} = X \setminus A \equiv \{ x\in X \mid x \not\in A\}.$

Свойства

• Операция дополнения является унарной операцией на булеане 2^X.
• Законы дополнения:

• $A \cup A^{\complement} = X;$
• $A \cap A^{\complement} = \emptyset;$

В частности, если оба A и 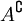$A^{\complement}$ непусты, то 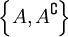$\left\{A,A^{\complement}\right\}$ является разбиением X.

• $X^{\complement} = \emptyset;$
• $\emptyset^{\complement}=X;$
• $(A \subset B) \Leftrightarrow \left(B^{\complement} \subset A^{\complement}\right).$

• Операция дополнения является инволюцией:

$\left(A^{\complement}\right)^{\complement} = A.$

• Законы де Моргана:

• $(A \cup B)^{\complement} = A^{\complement} \cap B^{\complement};$
• $(A \cap B)^{\complement} = A^{\complement} \cup B^{\complement}.$

• Законы разности множеств:

• $A \setminus B = A \cap B^{\complement};$
• $(A \setminus B)^{\complement} = A^{\complement} \cup B.$

См. также

• Операции над множествами