Накрывающей

Пример накрытия: накрытие $R\to S^1$ окружности S¹ спиралью, гомеоморфной пространству вещественных чисел R.

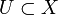Накрытие — это непрерывное сюръективное отображение $p:T\to X$ линейно связного пространства T на линейно связное пространство X, такое, что у любой точки $x \in X$ найдется окрестность $U\subset X$, полный прообраз которой p ^{− 1}(U) представляет собой объединение непересекающихся областей $V_k\subset T$:

$p^{-1}(U) = V_1\cup V_2\cup\dots$,

причем на каждой области V_k отображение $p:\,V_k\to U$ является гомеоморфизмом между V_k и U.

Формальное определение

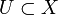Отображение $p:T\to X$ линейно связного топологического пространства T на линейно связное топологическое пространство X называется накрытием, если у любой точки $x\in X$ имеется окрестность $U\subset X$, для которой существует гомеоморфизм $h:p^{-1}(U)\to U\times \Gamma$, где Γ — дискретное пространство, такое что если $\pi:U\times \Gamma\to U$ обозначает естественную проекцию, то

$p|_{p^{-1}(U)}=\pi\circ h$.

Связанные определения

• Пространство X называется базой накрытия, а T — пространством накрытия (или накрывающим пространством).
• Прообраз p ^{− 1}(x) точки $x \in X$ называют слоем над точкой x.
• Число областей V_k в полном прообразе p ^{− 1}(U) называется числом листов.
  • Если это число конечно и равно n, то накрытие называется n-листным.
• Накрытие называется универсальным если накрывающее пространство односвязно.

Примеры

• Пусть S¹ обозначает единичную окружность комплексной плоскости $S^1=\{z\in {\mathbb C||z|=1}\}$.
  • $p: {\mathbb R}\to S^1$,   $p:x\mapsto e^{2\pi i x}$.
  • $p:S^1\to S^1$,   $p:z\mapsto z^k$, где $k\neq 0$, $k \in {\mathbb Z}$.

Свойства

• Накрытия являются локальными гомеоморфизмами
• Накрытия являются частным случаем локально тривиальных расслоений. Их можно рассматривать как локально тривиальные расслоения с дискретным слоем.
• Все двулистные накрытия регулярны.
• Универсальное накрытие регулярно.

Связь с фундаментальной группой

Обычно накрытие рассматривается в предположении связности X и Y и также локальной связности и локальной односвязности Y. При этих предположениях устанавливается связь между фундаментальными группами π₁(X,x₀) и π₁(Y,y₀): если p(x₀) = y₀, то индуцированный гомоморфизм $p:\pi_1(X,x_0)\to \pi_1(Y, y_0)$, отображает π₁(X,x₀) изоморфно на подгруппу в π₁(Y,y₀) и, меняя точку x₀ в p ^{− 1}(y₀), можно получить в точности все подгруппы из некоторого класса сопряженных подгрупп.

Если этот класс состоит из одной подгруппы H (т. е. H — нормальный делитель), то накрытие назывется регулярным. В этом случае возникает свободное действие группы G = π₁(Y,y₀) / H на X, причем p оказывается факторотображением на пространство орбит Y. Вообще, свободные действия дискретных групп — обычный источник регулярных накрытий (над пространством орбит, хотя и не всякое такое действие задает накрытие, пространство орбит может оказаться неотделимым), но это так для конечных групп. Это действие порождается поднятием петель: если петле $q:[0,1] \to Y$, q(0) = q(1) = y₀, сопоставить единственный путь $\tilde q: [0,1]\to X$, для которого q(0) = x₀ и $p\tilde q=q$, то точка $\tilde q(1)$ будет зависеть только от класса этой петли в G и от точки x₀. Таким образом, элементу из G отвечает перестановка точек в p ^{− 1}(y₀). Эта перестановка не имеет неподвижных точек, и непрерывно зависит от точки y₀. Это определяет гомеоморфизм X комутирующий с p.

В общем случае эта конструкция определяет лишь перестановку в p ^{− 1}(y₀), то есть имеется действие π₁(Y,y₀) на p ^{− 1}(y₀), назывемый монодромией накрытия. Частным случаем регулярного накрытия является универсальное накрытие, для которого G = π₁(Y,y₀) или, что эквивалентно, X — односвязно.

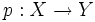Вообще, по каждой группе $H\subset \pi_1(Y, y_0)$ однозначно строится накрытие $p:X\to Y$, для которого образ π₁(X,x₀) есть H.

Для любого отображения f линейно связного пространства (Z,z₀) в (Y,y₀) поднятие его до отображения $\tilde f: (Z, z_0)\to (X,x_0)$ существует тогда и только тогда, когда образ f(π₁(Z,z₀)) лежит в H. Между накрытиями Y имеется отношение частичного порядка (накрытие накрытия есть накрытие), двойственное включению подгрупп в π₁(Y,y₀). В частности, универсальное накрытие является единственным максимальным элементом.

Литература

• Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. Методы и приложения. М.: Наука,1986
• В.Г.Болтянский, В.А.Ефремович, Наглядная топология выпуск 21 серии «Библиотечка квант» М., Наука, 1982.

См. также

• Локально тривиальное расслоение
• Фундаментальная группа