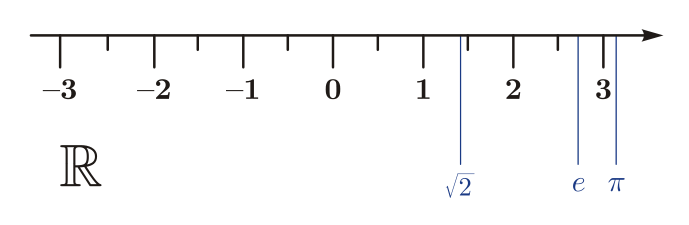
- Числовая ось
-
Числовая ось, или числовая прямая — это прямая, на которой выбраны:
- некоторая точка O — начало отсчёта;
- положительное направление, указанное стрелкой;
- масштаб для измерения длин.
Между вещественными числами и числовой осью устанавливается взаимно однозначное соответствие: начало координат соответствует нулю, числовое значение произвольной точки соответствует расстоянию её до начала координат — в положительном направлении со знаком плюс, иначе — со знаком минус.[1] Таким образом, числовая ось состоит из точки начала координат и двух расходящихся от неё лучей, один из которых соответствует положительным, а другой — отрицательным числам. Естественный порядок точек на прямой при таком соответствии согласуется с упорядоченностью чисел.
Числовая прямая часто используется как наглядный образ множества вещественных чисел
 (например, для построения графиков). Отрезки прямой при этом изображают числовые интервалы.
(например, для построения графиков). Отрезки прямой при этом изображают числовые интервалы.См. также
- Комплексная плоскость
- Числовой луч
- Ось координат
- Прямая Александрова (англ.)
- Прямая Суслина (англ.)
Примечания
- ↑ Существование точки-образа для любого вещественного числа гарантирует особая аксиома непрерывности, включаемая в современную аксиоматику геометрии.
Литература
- Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2003. — ISBN 5-17-009554-6
Категории:- Элементарная математика
- Числа
Wikimedia Foundation. 2010.