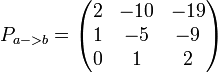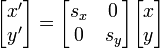Матрица перехода — У этого термина существуют и другие значения, см. Цепи Маркова#Переходная матрица и однородные цепи. Матрицей перехода от базиса к базису является матрица, столбцы которой координаты разложения векторов в базисе . Обозначается … Википедия
Разложение матрицы — Разложение матрицы представление матрицы в виде произведения матриц, обладающих некоторыми определёнными свойствами, например, ортогональностью, симметричностью, диагональностью и потому облегчающих рассмотрение свойств линейного… … Википедия
Подобные матрицы — Квадратные матрицы A и B одинакового порядка называются подобными, если существует невырожденная матрица P того же порядка, такая что: Подобные матрицы получаются при задании одного и того же линейного преобразования матрицей в разных… … Википедия
Подобные матрицы — квадратные матрицы (См. Матрица) А и В порядка n, связанные соотношением В = Р 1АР, где Р какая либо неособенная (т. е. имеющая обратную) матрица того же порядка. При задании матрицей линейного преобразования (См. Линейное преобразование) … Большая советская энциклопедия
скорость выщелачивания радионуклидов из цементной матрицы — 3.3 скорость выщелачивания радионуклидов из цементной матрицы: Скорость перехода радионуклидов в растворитель при контакте с последним. Источник: ГОСТ Р 51883 2002: Отходы радиоактивные цементированные. Общие технические требования … Словарь-справочник терминов нормативно-технической документации
ГИПЕРБОЛИЧЕСКОГО ТИПА УРАВНЕНИЕ — численные методы решения методы решения уравнений гииерболпч. типа на основе вычислительных алгоритмов. Различные математич. модели во многих случаях приводят к дифференциальным уравнениям гиперболич. типа. Такие уравнения имеют точные аиалитич.… … Математическая энциклопедия
Матрица поворота — Проверить информацию. Необходимо проверить точность фактов и достоверность сведений, изложенных в этой статье. На странице обсуждения должны быть пояснения … Википедия
Процесс Грама ― Шмидта — Процесс Грама (англ.) ― Шмидта это один из алгоритмов, в которых на основе счётного множества линейно независимых векторов строится множество ортогональных векторов или ортонормированных векторов , причём так, что каждый вектор … Википедия
Ортогонализация Грама-Шмидта — Процесс Грама ― Шмидта ― наиболее известный алгоритм ортогонализации, при котором по линейно независимой системе строится ортогональная система такая, что каждый вектор bi линейно выражается через , то есть матрица перехода от {ai} к {bi} ―… … Википедия
Ортогонализация Грама ― Шмидта — Процесс Грама ― Шмидта ― наиболее известный алгоритм ортогонализации, при котором по линейно независимой системе строится ортогональная система такая, что каждый вектор bi линейно выражается через , то есть матрица перехода от {ai} к {bi} ―… … Википедия
 .
. .
. .
.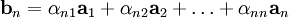 .
.
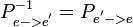
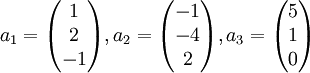 к единичному базису
к единичному базису  путём элементарных преобразований
путём элементарных преобразований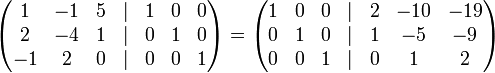 следовательно
следовательно