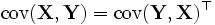Матрица ковариаций (для — 1.33. Матрица ковариаций (для n мерной случайной величины; n ³ 2) где дисперсия случайной величины Xi в одномерном маргинальном распределении (i = l, 2, ..., n), ковариация случайной величины (Xi, Xj) в двумерном маргинальном распределении (i … Словарь-справочник терминов нормативно-технической документации
Матрица ковариации — Ковариационная матрица (или матрица ковариаций) в теории вероятностей это матрица, составленная из попарных ковариаций элементов двух случайных векторов. Определения Пусть два случайных вектора размерности n и m соответственно. Пусть также… … Википедия
ИНФОРМАЦИОННАЯ МАТРИЦА — информация по Фишер у, матрица ковариаций информанта. Для доминированного семейства распределений вероятностей Pt(dw)с плотностями р(w; t), достаточно гладко зависящими от векторного (в частности, числового) параметра элементы И. м. при t= q… … Математическая энциклопедия
КОВАРИАЦИОННАЯ МАТРИЦА — матрица, образованная из попарных ковариаций нескольких случайных величин; точнее, для k мерного случайного вектора X=(X1,. .., Xk )К. м. наз. квадратная матрица где вектор средних значений. Компоненты К. м. равны и при i=j совпадают с DXi (т. е … Математическая энциклопедия
Ковариационная матрица — (или матрица ковариаций) в теории вероятностей это матрица, составленная из попарных ковариаций элементов одного или двух случайных векторов. Ковариационная матрица случайного вектора квадратная симметрическая матрица, на диагонали… … Википедия
Вариационно-ковариационная матрица — (VARIANCE COVARIANCE MATRIX) симметричная таблица ковариаций между некоторым числом случайных переменных. Дисперсии случайных переменных представлены на диагонали матрицы, а ковариаций выше и ниже диагонали … Финансовый глоссарий
КОВАРИАЦИОННАЯ МАТРИЦА — матрица, образованная из попарных смешанных вторых моментов (ковариаций) неск. случайных величин (см. Моменты случайной величины). Ковариация между компонентами и случайного вектора определяется как где М математическое ожидание, а … Физическая энциклопедия
СТРУКТУРНЫЕ УРАВНЕНИЯ — метод моделирования отношений между несколькими переменными зависимыми (далее ЗП) и независимыми (далее НП), измеренными и латентными, непрерывными и дискретными, оформившийся в 1970 х в работах статистиков (К. Йореског и Д. Сёрбом), социологов… … Социология: Энциклопедия
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
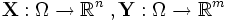 — два случайных вектора размерности n и m соответственно. Пусть также случайные величины
— два случайных вектора размерности n и m соответственно. Пусть также случайные величины 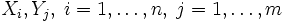 имеют конечный второй момент, то есть
имеют конечный второй момент, то есть 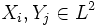 . Тогда матрицей ковариации векторов
. Тогда матрицей ковариации векторов 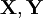 называется
называется![\sigma_{ij} = \mathrm{cov}(X_i,Y_j) \equiv \mathbb{E}\left[(X_i - \mathbb{E}X_i) (Y_j - \mathbb{E}Y_j)\right],\; i=1,\ldots, n,\; j = 1,\ldots, m](/pictures/wiki/files/49/18f60757eacfc6da968e99f186185c06.png) .
.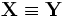 , то Σ называется матрицей ковариации вектора
, то Σ называется матрицей ковариации вектора 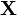 и обозначается
и обозначается 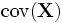 . Такая матрица ковариации является обобщением дисперсии для многомерной случайной величины, а ее след — скалярным выражением дисперсии многомерной случайной величины. Собственные векторы и собственные числа этой матрицы позволяют оценить размеры и форму облака распределения такой случайной величины, аппроксимировав его эллипсоидом (или эллипсом в двумерном случае).
. Такая матрица ковариации является обобщением дисперсии для многомерной случайной величины, а ее след — скалярным выражением дисперсии многомерной случайной величины. Собственные векторы и собственные числа этой матрицы позволяют оценить размеры и форму облака распределения такой случайной величины, аппроксимировав его эллипсоидом (или эллипсом в двумерном случае).![\mathrm{cov}(\mathbf{X}) = \mathbb{E}\left[\mathbf{X} \mathbf{X}^{\top}\right] - \mathbb{E}[\mathbf{X}] \cdot \mathbb{E}\left[\mathbf{X}^{\top}\right]](/pictures/wiki/files/102/fb27f2ac44f15197f8a4eb8910558c42.png) .
.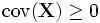 .
.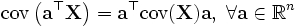 .
.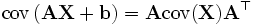 ,
,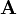 — произвольная матрица размера
— произвольная матрица размера 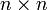 , а
, а 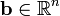 .
.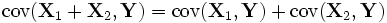 ,
,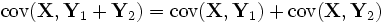 .
.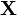 и
и 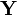 независимы, то
независимы, то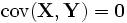 .
.
![\Sigma = \mathrm{cov}(\mathbf{X},\mathbf{Y}) = \mathbb{E}\left[(\mathbf{X} - \mathbb{E}\mathbf{X})(\mathbf{Y} - \mathbb{E}\mathbf{Y})^{\top}\right],](/pictures/wiki/files/99/c647c676e65db9126ed004cc1056f759.png)