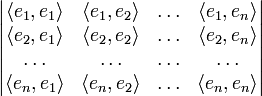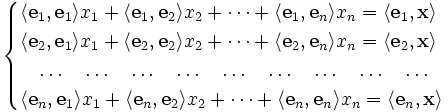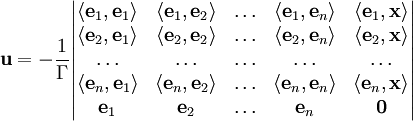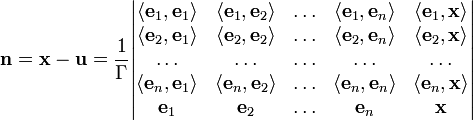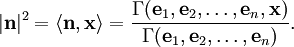- Матрица Грама
-
Определителем Грама системы векторов e1, e2, ..., en в евклидовом пространстве называется определитель матрицы Грама этой системы:
где
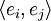 — скалярное произведение векторов ei и ej.
— скалярное произведение векторов ei и ej.Матрица Грама возникает из следующей задачи линейной алгебры:
Пусть в евклидовом пространстве V система векторов e1, e2, ..., en порождает подпространство U. Зная, чему равны скалярные произведения вектора x из U с каждым из этих векторов, найти коэффициенты разложения вектора x по векторам e1, e2, ..., en.
Исходя из разложения x = x1e1 + x2e2 + ... + xnen получается линейная система уравнений с матрицей Грама:Эта задача однозначно разрешима тогда и только тогда, когда векторы e1, e2, ..., en линейно независимы. Поэтому обращение в нуль определителя Грама системы векторов - это критерий их линейной зависимости.
Геометрический смысл определителя Грама
Геометрический смысл определителя Грама раскрывается при решении следующей задачи:
Пусть в евклидовом пространстве V система векторов e1, e2, ..., en порождает подпространство U. Зная скалярные произведения вектора x из V с каждым из этих векторов, найти расстояние от x до U.
Минимум расстояний |x-u| по всем векторам u из U достигается на ортогональной проекции вектора x на U. При этом x=u+n, где вектор n перпендикулярен всем векторам из U, и расстояние от x до U равно модулю вектора n. Для вектора u решается задача о разложении (см. выше) по векторам e1, e2, ..., en, и решение получившейся системы выписывается по правилу Крамера:где Г - определитель Грама системы. Вектор n равен:
и квадрат его модуля равен
Из этой формулы индукцией по n получается следующее утверждение:
- Определитель Грама системы n векторов равен квадрату n-мерного объёма параллелепипеда, натянутого на эти вектора.
Wikimedia Foundation. 2010.