- Идеальный газ
-
Термодинамика 
Статья является частью одноименной серии. Начала термодинамики Уравнение состояния Термодинамические величины Термодинамические потенциалы Термодинамические циклы Фазовые переходы править См. также «Физический портал» Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.
Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.
Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Дирака или Бозе — Эйнштейна).
Содержание
История
Существование атмосферного давления было показано рядом экспериментов в XVII веке. Одним из первых доказательств гипотезы стали магдебургские полушария, сконструированные немецким инженером Герике. Из сферы, образованной полушариями, выкачивался воздух, после чего их было трудно разъединить в силу внешнего давления воздуха. Другой эксперимент в рамках исследования природы атмосферного давления поставил Роберт Бойль. Он состоял в том, что если запаять изогнутую стеклянную трубку с короткого конца, а в длинное колено постоянно подливать ртуть, она не поднимется до верха короткого колена, поскольку воздух в трубке, сжимаясь, будет уравновешивать давление ртути на него. К 1662 году данные опыты позволили прийти к формулировке закона Бойля — Мариотта[1].
В 1802 году Гей-Люссаком был впервые опубликован в открытой печати закон объёмов (называемый в русскоязычной литературе законом Гей-Люссака) [2], однако сам Гей-Люссак считал, что открытие было сделано Жаком Шарлем в неопубликованной работе, относящейся к 1787 году. Независимо от них закон был открыт в 1801 году английским физиком Джоном Дальтоном. Кроме того, качественно закон был описан французом Гийомом Амонтоном в конце XVII века. Впоследствии он уточнил свои эксперименты и установил, что при изменении температуры от 0 до 100 °C объём воздуха линейно увеличивается на 0,375. Проведя аналогичные опыты с другими газами, Гей-Люссак установил, что это число одинаково для всех газов, несмотря на общепринятое мнение, что разные газы расширяются при нагревании различным образом.
В 1834 году из комбинации этих законов Клапейрон смог составить уравнение идеального газа[3]. Тот же закон, уже с использованием молекулярно-кинетической теории был сформулирован Августом Крёнигом в 1856 году[4] и Рудольфом Клаузиусом в 1857 году[5].
Классический идеальный газ
Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:
- Диаметр молекулы
 пренебрежимо мал по сравнению со средним расстоянием между ними (
пренебрежимо мал по сравнению со средним расстоянием между ними ( ) [6][7].
) [6][7]. - Импульс передается только при соударениях, то есть, силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях.
- Суммарная энергия частиц газа постоянна если нет передачи тепла или совершения газом работы.
В этом случае частицы газа движутся независимо друг от друга, давление газа на стенку равно сумме импульсов в единицу времени, переданной при столкновении частиц со стенкой, энергия — сумме энергий частиц газа.
По эквивалентной формулировке идеальный газ - такой газ, который одновременно подчиняется закону Бойля — Мариотта и Гей-Люссака[7], то есть:
где
 — давление,
— давление,  — абсолютная температура. Свойства идеального газа описываются уравнением Менделеева — Клапейрона
— абсолютная температура. Свойства идеального газа описываются уравнением Менделеева — Клапейрона-
-
-
 ,
,
-
-
где
 - универсальная газовая постоянная,
- универсальная газовая постоянная,  — масса,
— масса,  — молярная масса.
— молярная масса.или
где
 — концентрация частиц,
— концентрация частиц,  — постоянная Больцмана.
— постоянная Больцмана.Для любого идеального газа справедливо соотношение Майера:
где
 — универсальная газовая постоянная,
— универсальная газовая постоянная,  — молярная теплоемкость при постоянном давлении,
— молярная теплоемкость при постоянном давлении,  — молярная теплоемкость при постоянном объёме.
— молярная теплоемкость при постоянном объёме.Применение теории идеального газа
Физический смысл температуры газа
Так как давление молекул газа на стенку определяется по формуле
 , где
, где  - средняя кинетическая энергия поступательного движения молекул газа. Подставив это в уравнение Менделеева — Клапейрона получаем, что температура пропорциональна
- средняя кинетическая энергия поступательного движения молекул газа. Подставив это в уравнение Менделеева — Клапейрона получаем, что температура пропорциональна  .
.Распределение Больцмана
Равновесное распределение частиц классического идеального газа по состояниям следует из уравнения Менделеева — Клапейрона, из которого можно вывести распределение газа в поле потенциальной энергии. Это распределение приводит к распределению Больцмана:
где
 — среднее число частиц, находящихся в
— среднее число частиц, находящихся в  -ом состоянии с энергией
-ом состоянии с энергией  , а константа
, а константа  определяется условием нормировки:
определяется условием нормировки:где
 — полное число частиц.
— полное число частиц.Распределение Больцмана является предельным случаем (квантовые эффекты пренебрежимо малы) распределений Ферми — Дирака и Бозе — Эйнштейна, и, соответственно, классический идеальный газ является предельным случаем Ферми-газа и Бозе-газа.
Адиабатический процесс
C помощью модели идеального газа можно предсказать изменение параметров состояния газа при адиабатическом процессе. Перепишем уравнение в виде:
Продифференцировав обе части, получаем:
Затем, если подставить в это уравнение значение работы и внутренней энергии газа, получим Уравнение Пуассона.
Квантовый идеальный газ
Понижение температуры и увеличение плотности газа может привести к ситуации, когда среднее расстояние между частицами становится соизмеримым с длиной волны де Бройля для этих частиц, что приводит к переходу от классического к квантовому идеальному газу (см. Вырожденный газ). В таком случае поведение газа зависит от спина частиц: в случае полуцелого спина (фермионы) действует статистика Ферми — Дирака (Ферми-газ), в случае целого спина (бозоны) — статистика Бозе — Эйнштейна (Бозе-газ).
Ферми-газ
Для фермионов действует принцип Паули, запрещающий двум тождественным фермионам находиться в одном квантовом состоянии. Вследствие этого при абсолютном нуле температуры импульсы частиц и, соответственно, давление и плотность энергии Ферми-газа отличны от нуля и пропорциональны числу частиц в единице объёма. Существует верхний предел энергии, который могут иметь частицы Ферми-газа при абсолютном нуле (Энергия Ферми
 ). Если энергия теплового движения частиц Ферми-газа значительно меньше энергии Ферми, то это состояние называют вырожденным газом.
). Если энергия теплового движения частиц Ферми-газа значительно меньше энергии Ферми, то это состояние называют вырожденным газом.Особенностью Ферми-газов является крайне слабая зависимость давления от температуры: в нерелятивистском случае давление
 , в релятивистском —
, в релятивистском —  .
.Примерами Ферми-газов являются электронный газ в металлах, сильнолегированных и вырожденных полупроводниках, вырожденный газ электронов в белых карликах и вырожденный газ нейтронов в нейтронных звёздах.
Бозе-газ
Так как на бозоны могут быть строго тождественны друг другу[8][9] и, соответственно, принцип Паули на них не распространяется, то при снижении температуры Бозе-газа ниже некоторой температуры
 возможен переход бозонов на наинизший энергетический уровень с нулевым импульсом, то есть образование конденсата Бозе — Эйнштейна. Поскольку давление газа равно сумме импульсов частиц, переданной стенке в единицу времени, при
возможен переход бозонов на наинизший энергетический уровень с нулевым импульсом, то есть образование конденсата Бозе — Эйнштейна. Поскольку давление газа равно сумме импульсов частиц, переданной стенке в единицу времени, при  давление Бозе-газа зависит только от температуры.Этот эффект в 1995 году наблюдался экспериментально, а в 2001 году авторам эксперимента была присуждена Нобелевская премия[10].
давление Бозе-газа зависит только от температуры.Этот эффект в 1995 году наблюдался экспериментально, а в 2001 году авторам эксперимента была присуждена Нобелевская премия[10].Примерами Бозе-газов являются различного рода газы квазичастиц (слабых возбуждений) в твёрдых телах и жидкостях, сверхтекучая компонента гелия II, конденсата Бозе — Эйнштейна куперовских электронных пар при сверхпроводимости. Примером ультрарелятивистского Бозе-газа является фотонный газ[8][9].

См. также
Примечания
- ↑ Кудрявцев, 1956, с. 185—186
- ↑ Gay-Lussac, J. L. Recherches sur la dilatation des gaz et des vapeurs // Annales de chimie. — 1802. — Vol. XLIII. — P. 137.
- ↑ Clapeyron, E. (1834). «Mémoire sur la puissance motrice de la chaleur». Journal de l'École Polytechnique XIV: 153–90. (фр.) Facsimile at the Bibliothèque nationale de France (pp. 153–90).
- ↑ Krönig, A. (1856). «Grundzüge einer Theorie der Gase». Annalen der Physik 99 (10): 315–22. DOI:10.1002/andp.18561751008. Bibcode: 1856AnP...175..315K. (нем.) Facsimile at the Bibliothèque nationale de France (pp. 315–22).
- ↑ Clausius, R. (1857). «Ueber die Art der Bewegung, welche wir Wärme nennen». Annalen der Physik und Chemie 176 (3): 353–79. DOI:10.1002/andp.18571760302. Bibcode: 1857AnP...176..353C. (нем.) Facsimile at the Bibliothèque nationale de France (pp. 353–79).
- ↑ Коган М. Н. Динамика разреженного газа (кинетическая теория. М., 1967)
- ↑ 1 2 Савельев, 2001, с. 24
- ↑ 1 2 Einstein A. (1924). «Quantentheorie des einatomigen idealen Gases». Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse 1924: 261—267. (нем.)
- ↑ 1 2 Einstein A. (1925). «Quantentheorie des einatomigen idealen Gases, Zweite Abhandlung». Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse 1925: 3—14. (нем.)
- ↑ Anderson, M. H.; Ensher, J. R.; Matthews, M. R.; Wieman, C. E.; Cornell, E. A. (1995). «Observation of Bose–Einstein Condensation in a Dilute Atomic Vapor». Science 269: 198—201. DOI:10.1126/science.269.5221.198. PMID 17789847. (англ.)
Литература
- Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9
- П. С. Кудрявцев История физики. — М.: Гос. учебно-педагог. изд-во, 1956. — Т. 1. От античной физики до Менделеева. — 564 с. — 25 000 экз.
- V.P.Maslov, Mathematical conception of the gas theory
Категории:- Термодинамика
- Статистическая физика
- Математические модели
- Идеализации в физике
- Газ
- Диаметр молекулы
Wikimedia Foundation. 2010.


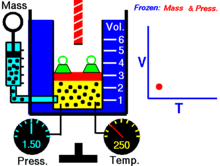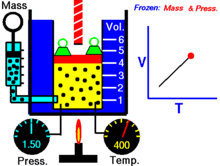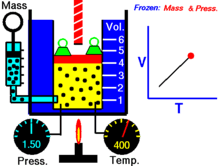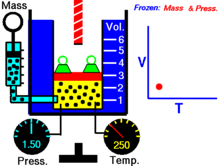







 диаграмме для газа.
диаграмме для газа. — давление газа;
— давление газа; — объём.
— объём.

