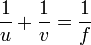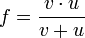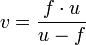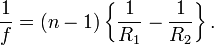- Линза (оптика)
-
Линза (нем. Linse, от лат. lens — чечевица) — обычно — диск из прозрачного однородного материала, ограниченный двумя полированными поверхностями — сферическими или плоской и сферической. В настоящее время всё чаще применяются и т. н. «асферические линзы», форма поверхности которых отличается от сферы.
Линзами называют и другие оптические приборы и явления, которые создают сходный оптический эффект, не обладая указанными внешними характеристиками. Например:
- Плоские «линзы», изготовленные из материала с переменным коэффициентом преломления, изменяющимся в зависимости от расстояния от центра
- линзы Френеля
- зонная пластинка Френеля, использующая явление дифракции
- «линзы» воздуха в атмосфере — неоднородность свойств, в частности коэффициента преломления (проявляются в виде мерцания изображения звёзд в ночном небе).
- Гравитационная линза — наблюдаемый на межгалактических расстояниях эффект отклонения электромагнитных волн массивными объектами.
- Электростатическая линза — электрическое поле, сформированное таким образом, чтобы фокусировать пучок электронов, например, в электронном микроскопе.
- Изображение линзы, сформированное оптической системой или частью оптической системы. Используется при расчёте сложных оптических систем.
В качестве материала линз, чаще всего, используются оптические материалы, такие как стекло, оптическое стекло, оптически прозрачные пластмассы и другие материалы.
История
Первое упоминание о линзах можно найти в древнегреческой пьесе Аристофана «Облака» (424 до н. э.), где с помощью выпуклого стекла и солнечного света добывали огонь.
Из произведений Плиния Старшего (23 — 79) следует, что такой способ разжигания огня был известен и в Римской империи — там также описан, возможно, первый случай применения линз для коррекции зрения — известно, что Нерон смотрел гладиаторские бои через вогнутый изумруд для исправления близорукости.
Сенека (3 до н. э. — 65) описал увеличительный эффект, который даёт стеклянный шар, заполненный водой.
Арабский математик Альхазен (965—1038) написал первый значительный трактат по оптике, описывающий, как хрусталик глаза создаёт изображение на сетчатке. Линзы получили широкое использование лишь с появлением очков примерно в 1280-х годах в Италии.
Характеристики тонких линз
В зависимости от форм различают собирательные (положительные) и рассеивающие (отрицательные) линзы. К группе собирательных линз обычно относят линзы, у которых середина толще их краёв, а к группе рассеивающих — линзы, края которых толще середины. Следует отметить, что это верно только если показатель преломления у материала линзы больше, чем у окружающей среды. Если показатель преломления линзы меньше, ситуация будет обратной. Например пузырёк воздуха в воде — двояковыпуклая рассеивающая линза.
Линзы характеризуются, как правило, своей оптической силой (измеряется в диоптриях), или фокусным расстоянием.
Для построения оптических приборов с исправленной оптической аберрацией (прежде всего — хроматической, обусловленной дисперсией света, — ахроматы и апохроматы) важны и иные свойства линз/их материалов, например, коэффициент преломления, коффициент дисперсии, коэффициент пропускания материала в выбранном оптическом диапазоне.
Иногда линзы/линзовые оптические системы (рефракторы) специально рассчитываются на использование в средах с относительно высоким коэффициентом преломления (см. иммерсионный микроскоп, иммерсионные жидкости).
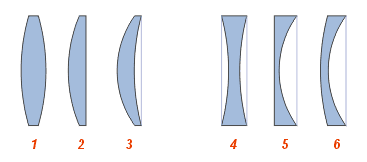 Виды линз:
Виды линз:
Собирающие:
1 — двояковыпуклая
2 — плоско-выпуклая
3 — вогнуто-выпуклая (положительный мениск)
Рассеивающие:
4 — двояковогнутая
5 — плоско-вогнутая
6 — выпукло-вогнутая (отрицательный мениск)
Выпукло-вогнутая линза называется мениском и может быть собирательной (утолщается к середине) или рассеивающей (утолщается к краям). Мениск, у которого радиусы поверхностей равны, имеет оптическую силу, равную нулю (применяется для коррекции дисперсии или как покровная линза). Так, линзы очков для близоруких — как правило, отрицательные мениски.Отличительным свойством собирательной линзы является способность собирать падающие на её поверхность лучи в одной точке, расположенной по другую сторону линзы.
 Основные элементы линзы: NN — главная оптическая ось — прямая линия, проходящая через центры сферических поверхностей, ограничивающих линзу; O — оптический центр — точка, которая у двояковыпуклых или двояковогнутых (с одинаковыми радиусами поверхностей) линз находится на оптической оси внутри линзы (в её центре).
Основные элементы линзы: NN — главная оптическая ось — прямая линия, проходящая через центры сферических поверхностей, ограничивающих линзу; O — оптический центр — точка, которая у двояковыпуклых или двояковогнутых (с одинаковыми радиусами поверхностей) линз находится на оптической оси внутри линзы (в её центре).
Примечание. Ход лучей показан, как в идеализированной (плоской) линзе, без указания на преломление на реальной границе раздела фаз. Дополнительно показан несколько утрированный образ двояковыпуклой линзыЕсли на некотором расстоянии перед собирательной линзой поместить светящуюся точку S, то луч света, направленный по оси, пройдёт через линзу не преломившись, а лучи, проходящие не через центр, будут преломляться в сторону оптической оси и пересекутся на ней в некоторой точке F, которая и будет изображением точки S. Эта точка носит название сопряжённого фокуса, или просто фокуса.
Если на линзу будет падать свет от очень удалённого источника, лучи которого можно представить идущими параллельным пучком, то по выходе из неё лучи преломятся под бо́льшим углом и точка F переместится на оптической оси ближе к линзе. При данных условиях точка пересечения лучей, вышедших из линзы, называется главным фокусом F’, а расстояние от центра линзы до главного фокуса — главным фокусным расстоянием.
Лучи, падающие на рассеивающую линзу, по выходе из неё будут преломляться в сторону краёв линзы, то есть рассеиваться. Если эти лучи продолжить в обратном направлении так, как показано на рисунке пунктирной линией, то они сойдутся в одной точке F, которая и будет фокусом этой линзы. Этот фокус будет мнимым.
 Мнимый фокус рассеивающей линзы
Мнимый фокус рассеивающей линзыСказанное о фокусе на главной оптической оси в равной степени относится и к тем случаям, когда изображение точки находится на побочной или наклонной оптической оси, т. е. линии, проходящей через центр линзы под углом к главной оптической оси. Плоскость, перпендикулярная главной оптической оси, расположенная в главном фокусе линзы, называется главной фокальной плоскостью, а в сопряжённом фокусе — просто фокальной плоскостью.
Собирательные линзы могут быть направлены к предмету любой стороной, вследствие чего лучи по прохождении через линзу могут собираться как с одной, так и с другой её стороны. Таким образом, линза имеет два фокуса — передний и задний. Расположены они на оптической оси по обе стороны линзы на фокусном расстоянии от центра линзы.
Построение изображения тонкой собирающей линзой
При изложении характеристики линз был рассмотрен принцип построения изображения светящейся точки в фокусе линзы. Лучи, падающие на линзу слева, проходят через её задний фокус, а падающие справа — через передний фокус. Следует учесть, что у рассеивающих линз, наоборот, задний фокус расположен спереди линзы, а передний позади.

Построение линзой изображения предметов, имеющих определённую форму и размеры, получается следующим образом: допустим, линия AB представляет собой объект, находящийся на некотором расстоянии от линзы, значительно превышающем её фокусное расстояние. От каждой точки предмета через линзу пройдёт бесчисленное количество лучей, из которых, для наглядности, на рисунке схематически изображён ход только трёх лучей.
Три луча, исходящие из точки A, пройдут через линзу и пересекутся в соответствующих точках схода на A1B1, образуя изображение. Полученное изображение является действительным и перевёрнутым.
В данном случае изображение получено в сопряжённом фокусе в некоторой фокальной плоскости FF, несколько удалённой от главной фокальной плоскости F’F’, проходящей параллельно ей через главный фокус.
Далее приведены различные случаи построения изображений предмета, помещённого на различных расстояниях от линзы.
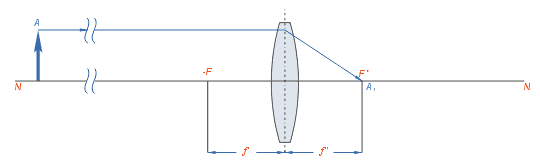 Если предмет находится на бесконечно далёком от линзы расстоянии, то его изображение получается в заднем фокусе линзы F’ действительным, перевёрнутым и уменьшенным до подобия точки.
Если предмет находится на бесконечно далёком от линзы расстоянии, то его изображение получается в заднем фокусе линзы F’ действительным, перевёрнутым и уменьшенным до подобия точки.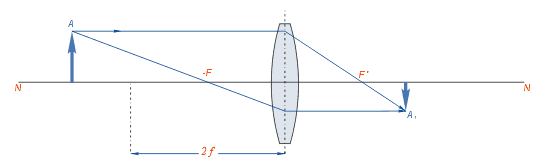 Если предмет приближён к линзе и находится на расстоянии, превышающем двойное фокусное расстояние линзы, то изображение его будет действительным, перевёрнутым и уменьшенным и расположится за главным фокусом на отрезке между ним и двойным фокусным расстоянием.
Если предмет приближён к линзе и находится на расстоянии, превышающем двойное фокусное расстояние линзы, то изображение его будет действительным, перевёрнутым и уменьшенным и расположится за главным фокусом на отрезке между ним и двойным фокусным расстоянием. Если предмет помещён на двойном фокусном расстоянии от линзы, то полученное изображение находится по другую сторону линзы на двойном фокусном расстоянии от неё. Изображение получается действительным, перевёрнутым и равным по величине предмету.
Если предмет помещён на двойном фокусном расстоянии от линзы, то полученное изображение находится по другую сторону линзы на двойном фокусном расстоянии от неё. Изображение получается действительным, перевёрнутым и равным по величине предмету.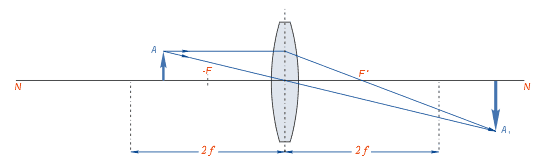 Если предмет помещён между передним фокусом и двойным фокусным расстоянием, то изображение будет получено за двойным фокусным расстоянием и будет действительным, перевёрнутым и увеличенным.
Если предмет помещён между передним фокусом и двойным фокусным расстоянием, то изображение будет получено за двойным фокусным расстоянием и будет действительным, перевёрнутым и увеличенным.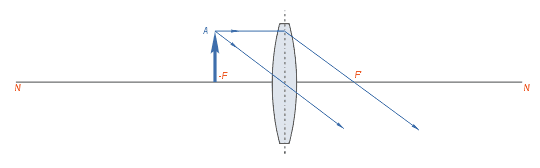 Если предмет находится в плоскости переднего главного фокуса линзы, то лучи, пройдя через линзу, пойдут параллельно, и изображение может получиться лишь в бесконечности.
Если предмет находится в плоскости переднего главного фокуса линзы, то лучи, пройдя через линзу, пойдут параллельно, и изображение может получиться лишь в бесконечности.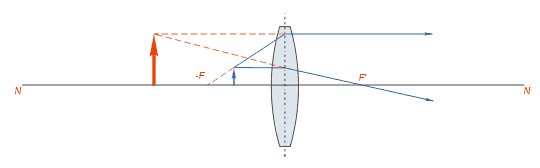 Если предмет поместить на расстоянии, меньшем главного фокусного расстояния, то лучи выйдут из линзы расходящимся пучком, нигде не пересекаясь. Изображение при этом получается мнимое, прямое и увеличенное, т. е. в данном случае линза работает как лупа.
Если предмет поместить на расстоянии, меньшем главного фокусного расстояния, то лучи выйдут из линзы расходящимся пучком, нигде не пересекаясь. Изображение при этом получается мнимое, прямое и увеличенное, т. е. в данном случае линза работает как лупа.Нетрудно заметить, что при приближении предмета из бесконечности к переднему фокусу линзы изображение удаляется от заднего фокуса и по достижении предметом плоскости переднего фокуса оказывается в бесконечности от него.
Эта закономерность имеет большое значение в практике различных видов фотографических работ, поэтому для определения зависимости между расстоянием от предмета до линзы и от линзы до плоскости изображения необходимо знать основную формулу линзы.
Формула тонкой линзы
Расстояния от точки предмета до центра линзы и от точки изображения до центра линзы называются сопряжёнными фокусными расстояниями.
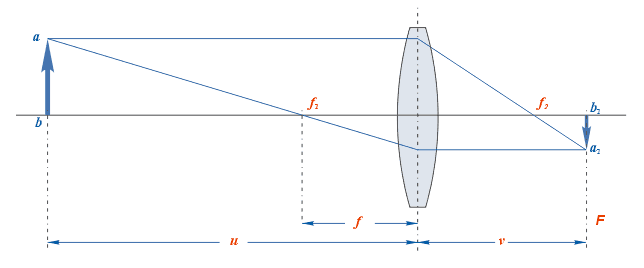
Эти величины находятся в зависимости между собой и определяются формулой, называемой формулой тонкой линзы:
где
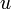 — расстояние от линзы до предмета;
— расстояние от линзы до предмета; 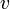 — расстояние от линзы до изображения;
— расстояние от линзы до изображения; 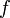 — главное фокусное расстояние линзы. В случае толстой линзы формула остаётся без изменения с той лишь разницей, что расстояния отсчитываются не от центра линзы, а от главных плоскостей.
— главное фокусное расстояние линзы. В случае толстой линзы формула остаётся без изменения с той лишь разницей, что расстояния отсчитываются не от центра линзы, а от главных плоскостей.Для нахождения той или иной неизвестной величины при двух известных пользуются следующими уравнениями:
Следует отметить, что знаки величин u, v, f выбираются исходя из следующих соображений — для действительного изображения от действительного предмета в собирающей линзе — все эти величины положительны. Если изображение мнимое — расстояние до него принимается отрицательным, если предмет мнимый — расстояние до него отрицательно, если линза рассеивающая — фокусное расстояние отрицательно.
Масштаб изображения
Масштабом изображения (
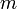 ) называется отношение линейных размеров изображения к соответствующим линейным размерам предмета. Это отношение может быть косвенно выражено дробью
) называется отношение линейных размеров изображения к соответствующим линейным размерам предмета. Это отношение может быть косвенно выражено дробью 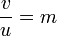 , где
, где 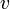 — расстояние от линзы до изображения;
— расстояние от линзы до изображения; 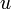 — расстояние от линзы до предмета.
— расстояние от линзы до предмета.Здесь
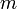 есть коэффициент уменьшения, т. е. число, показывающее во сколько раз линейные размеры изображения меньше действительных линейных размеров предмета.
есть коэффициент уменьшения, т. е. число, показывающее во сколько раз линейные размеры изображения меньше действительных линейных размеров предмета.В практике вычислений гораздо удобнее это соотношение выражать в значениях
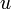 или
или 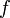 , где
, где 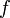 — фокусное расстояние линзы.
— фокусное расстояние линзы.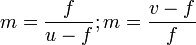 .
.Расчёт фокусного расстояния и оптической силы линзы

Значение фокусного расстояния для линзы может быть рассчитано по следующей формуле:
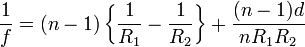 , где
, где
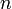 — коэффициент преломления материала линзы,
— коэффициент преломления материала линзы,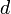 — расстояние между сферическими поверхностями линзы вдоль оптической оси, также известное как толщина линзы. Если
— расстояние между сферическими поверхностями линзы вдоль оптической оси, также известное как толщина линзы. Если 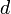 намного меньше, чем R1 и R2, то такая линза называется тонкой, и её фокусное расстояние можно найти как:
намного меньше, чем R1 и R2, то такая линза называется тонкой, и её фокусное расстояние можно найти как:(Эту формулу также называют формулой тонкой линзы.) Величина фокусного расстояния положительна для собирающих линз, и отрицательна для рассеивающих. Величина
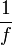 называется оптической силой линзы. Оптическая сила линзы измеряется в диоптриях, единицами измерения которых являются м−1.
называется оптической силой линзы. Оптическая сила линзы измеряется в диоптриях, единицами измерения которых являются м−1.Указанные формулы могут быть получены аккуратным рассмотрением процесса построения изображения в линзе с использованием закона Снелла, если перейти от общих тригонометрических формул к параксиальному приближению.
Линзы симметричны, то есть они имеют одинаковое фокусное расстояние независимо от направления света — слева или справа, что, однако, не относится к другим характеристикам, например, аберрациям, величина которых зависит от того, какой стороной линза повёрнута к свету.
Комбинация нескольких линз (центрированная система)
Линзы могут комбинироваться друг с другом для построения сложных оптических систем. Оптическая сила системы из двух линз может быть найдена как простая сумма оптических сил каждой линзы (при условии, что обе линзы можно считать тонкими и они расположены вплотную друг к другу на одной оси):
 .
.
Если линзы расположены на некотором расстоянии друг от друга и их оси совпадают (система из произвольного числа линз, обладающих таким свойством, называется центрированной системой), то их общую оптическую силу с достаточной степенью точности можно найти из следующего выражения:
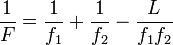 ,
,
где
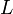 — расстояние между главными плоскостями линз.
— расстояние между главными плоскостями линз.Недостатки простой линзы
В современной фотоаппаратуре к качеству изображения предъявляются высокие требования.
Изображение, даваемое простой линзой, в силу целого ряда недостатков не удовлетворяет этим требованиям. Устранение большинства недостатков достигается соответствующим подбором ряда линз в центрированную оптическую систему — объектив. Изображения, полученные при помощи простых линз, имеют различные недостатки. Недостатки оптических систем называются аберрациями, которые делятся на следующие виды:
- Геометрические аберрации
- Хроматическая аберрация;
- Дифракционная аберрация (эта аберрация вызывается другими элементами оптической системы, и к самой линзе отношения не имеет).
Линзы со специальными свойствами
Линзы из органических полимеров
Полимеры дают возможность создавать недорогие асферические линзы с помощью литья.
Линзы контактныеВ области офтальмологии созданы мягкие контактные линзы. Их производство основано на применении материалов, имеющих бифазную природу, сочетающих фрагменты кремний-органического или кремний-фторорганического полимера силикона и гидрофильного полимера гидрогеля. Работа в течении более 20 лет привела к созданию в конце 90-х годов силикон-гидрогелевых линз, которые благодаря сочетанию гидрофильных свойств и высокой кислородопроницаемости могут непрерывно использоваться в течение 30 дней круглосуточно. [1]
Линзы из кварца
Кварцевое стекло — переплавленный чистый кремнезём с незначительными (около 0,01 %) добавками Al2О3, СаО и MgO. Оно отличается высокой термостойкостью и инертностью ко многим химическим реактивам за исключением плавиковой кислоты.
Прозрачное кварцевое стекло хорошо пропускает ультрафиолетовые и видимые лучи света.
Линзы из кремния
Кремний сочетает сверхвысокую дисперсию с самым большим абсолютным значением коэффициента преломления n=3,4 в диапазоне ИК-излучения и полной непрозрачностью в видимом диапазоне спектра.[2]
Кроме того, именно свойства кремния и новейшие технологии его обработки позволили создать линзы для рентгеновского диапазона электромагнитных волн.
Применение линз
Линзы являются универсальным оптическим элементом большинства оптических систем.
Традиционное применение линз — бинокли, телескопы, оптические прицелы, теодолиты, микроскопы и фотовидеотехника. Одиночные собирающие линзы используются как увеличительные стёкла.
Другая важная сфера применения линз офтальмология, где без них невозможно исправление недостатков зрения — близорукости, дальнозоркости, неправильной аккомодации, астигматизма и других заболеваний. Линзы используют в таких приспособлениях, как очки и контактные линзы.
В радиоастрономии и радарах часто используются диэлектрические линзы, собирающие поток радиоволн в приёмную антенну, либо фокусирующие на цели.
В конструкции плутониевых ядерных бомб для преобразования сферической расходящейся ударной волны от точечного источника (детонатора) в сферическую сходящуюся применялись линзовые системы, изготовленные из взрывчатки с разной скоростью детонации (то есть с разным коэффициентом преломления).
См. также
- Линза Френеля
- Линза Габора
- Линза Люнеберга
- Линза Бийе
- Линза Итона — Липмана
- Цейс, Карл
- Оптические системы
- Оптические материалы
Примечания
Ссылки
Литература
- Краткий фотографический справочник. Под общей редакцией д.т. н. Пуськова В. В., изд. 2-е, М., Искусство, 1953.
- Оптика, Г. С. Ландсберг, изд. 5-ое, М., Наука, 1976.
- Политехнический словарь, глав.ред. А. Ю. Ишлинский, изд. 3-е, М., Советская Энциклопедия, 1989.
- Линза // Фотокинотехника: Энциклопедия / Главный редактор Е. А. Иофис. — М.: Советская энциклопедия, 1981.
Wikimedia Foundation. 2010.