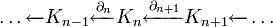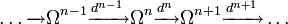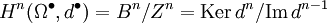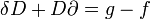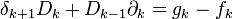- Коцепной комплекс
-
Цепно́й компле́кс — основное понятие гомологической алгебры.
Содержание
Цепной комплекс
Цепной комплексом называется последовательность
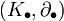 модулей и гомоморфизмов
модулей и гомоморфизмов 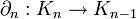 , называемых граничными операторами или дифференциалами,
, называемых граничными операторами или дифференциалами,такая что
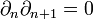 . Элементы Kn называются n-мерными цепями, элементы ядра
. Элементы Kn называются n-мерными цепями, элементы ядра 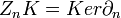 — n-мерными циклами, элементы образа
— n-мерными циклами, элементы образа 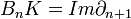 — n-мерными границами. Из
— n-мерными границами. Из 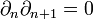 следует, что
следует, что 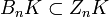 (т.н.полуточность). Если к тому же BnK = ZnK, то такой комплекс называется точным.
(т.н.полуточность). Если к тому же BnK = ZnK, то такой комплекс называется точным.Цепные комплексы модулей над фиксированным кольцом образуют категорию с мофизмами
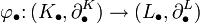 , где
, где 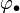 последовательность морфизмов
последовательность морфизмов 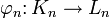 , такая что
, такая что 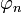 коммутирует с дифференциалом, то есть
коммутирует с дифференциалом, то есть 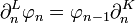 .
.Коцепной комплекс
Коцепной комплекс — понятие, двойственное цепному комплексу. Он определяется как последовательность модулей
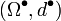 и гомоморфизмов
и гомоморфизмов 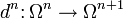 , таких что
, таких что- dn + 1dn = 0
Коцепной комплекс, как и цепной, является полуточной последовательностью.
Свойства и понятия, связанные с коцепными комплексами, двойственны аналогичным понятиям и свойствам цепных комплексов.
Гомологии и когомологии
n-мерная группа гомологий Hn цепного комплекса
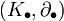 является его мерой точности в n-ом члене и определяется как
является его мерой точности в n-ом члене и определяется как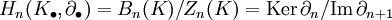 . Для точного комплекса Hn = 0
. Для точного комплекса Hn = 0
Аналогично определяется n-мерная группа когомологий коцепного комплекса:
Гомоморфизмы цепных комплексов
Гомоморфизмом цепных комплексов
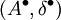 и
и 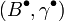 называется такое отображение
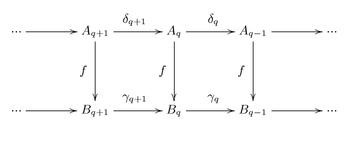
называется такое отображение 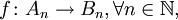 что следующая диаграмма оказывается коммутативной:
что следующая диаграмма оказывается коммутативной:Гомоморфизм цепных комплексов индуцирует гомоморфизм их групп гомологий.
Цепная гомотопия
Цепная гомотопия
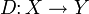 между гомоморфизмами комплексов f и g - это такой гомоморфизм цепных комплексов
между гомоморфизмами комплексов f и g - это такой гомоморфизм цепных комплексов 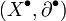 и
и 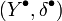 степени +1 (т.е.
степени +1 (т.е. 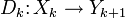 ), для которого
), для которогоДля коцепных комплексов соответствующая коммутативная диаграмма имеет вид
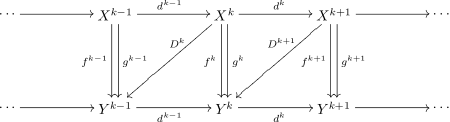
Литература
- Картан А., Эйленберг С. Гомологическая алгебра, — М.: Издательство Иностранной Литературы, 1960.
- Маклейн С. Гомология, — М.: Мир, 1966.
- Дольд А. Лекции по алгебраической топологии, — М.: Мир, 1976.
Wikimedia Foundation. 2010.