- Декартов лист
-
Декартов лист — плоская кривая третьего порядка, удовлетворяющая уравнению в прямоугольной системе
 . Параметр
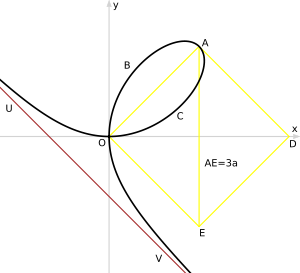
. Параметр  определяется как диагональ квадрата, сторона которого равна наибольшей хорде петли.
определяется как диагональ квадрата, сторона которого равна наибольшей хорде петли.Содержание
История
Впервые уравнение кривой исследовал Р. Декарт в 1638 году, однако он построил только петлю в первом координатном угле, где
 и
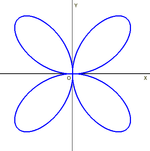
и  принимают положительные значения. Декарт полагал, что петля симметрично повторяется во всех четырёх координатных четвертях, в виде четырёх лепестков цветка. В то время эта кривая называлась цветком жасмина (англ. jasmine flower, фр. fleur de jasmin).
принимают положительные значения. Декарт полагал, что петля симметрично повторяется во всех четырёх координатных четвертях, в виде четырёх лепестков цветка. В то время эта кривая называлась цветком жасмина (англ. jasmine flower, фр. fleur de jasmin).В современном виде эту кривую впервые представил Х. Гюйгенс в 1692 году.
Уравнения
- В прямоугольной системе по определению:
 .
.
- Параметрическое уравнение в прямоугольной системе:
 , где
, где  .
.
Часто рассматривают повёрнутую на
 кривую. Её уравнения выглядят так:
кривую. Её уравнения выглядят так:- В прямоугольной системе:
 , где
, где 
- Параметрическое:
- В полярных координатах:
Вывод уравнений повёрнутой кривой Систему координат XOY преобразуют в систему координат UOV, которая получается поворотом осей OX и OY по часовой стрелке на угол  и переориентацией оси OX в противоположном направлении:
и переориентацией оси OX в противоположном направлении:
Выражение старых координат XY через новые UV выглядит так:

 , или
, или

 ,
,
После подстановки выражений старых координат через новые уравнение декартова листа преобразуется к следующему виду:
 .
.
Вводим параметр
 , последнее уравнение перепишется так:
, последнее уравнение перепишется так:или
 .
.
Заменяем переменные u и v на привычные x и y и получаем уравнение декартового листа в новой системе координат:
Подставив в уравнение предыдущее
 , получаем уравнение декартова листа в полярной системе координат:
, получаем уравнение декартова листа в полярной системе координат: .
.
Решая данное выражение относительно
 , получаем:
, получаем: .
.
Свойства
- Прямая
 — ось симметрии, её уравнение:
— ось симметрии, её уравнение:  .
. - Точка A называется вершиной, её координаты
 .
.
- Для обеих ветвей существует асимптота
 , её уравнение:
, её уравнение:  .
.
Вывод уравнения асимптоты Для повёрнутого декартового листа: При
 имеем
имеем или
или  ,
,
Рассматриваем второй случай:
 , то есть,
, то есть,  , то есть
, то есть  , значит
, значит  .
.Уравнение асимптоты UV определяется из выражения:
 , следовательно,
, следовательно,  .
.
После поворота осей на
 получаем окончательное уравнение
получаем окончательное уравнение- Площадь области между дугами
 и
и 

Нахождение площади 
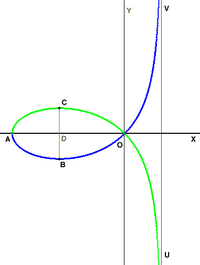
Площадь  , заключённая между дугами ACO и ABO вычисляется так:
, заключённая между дугами ACO и ABO вычисляется так:
 , где
, где  .
.
Этот интеграл вычисляется с помощью подстановки:
 .
.
Пределы интегрирования:
Интеграл преобразуется к виду:
или
Первый интеграл из этого уравнения:
 .
.
Подстановка:
 .
.
Пределы интегрирования:
 .
.
Интеграл преобразуется к виду:

![= \frac{2l}{ \sqrt{3}} \left[ \frac{v}{2} \sqrt{ \left( 2 \sqrt{t} \right)^2 - v^2} + \frac{ \left(2 \sqrt{l} \right)^2}{2} \arcsin \left( \frac{v}{2 \sqrt{l}} \right) \right] \Bigg|^\sqrt{l}_{2\sqrt{l}} = \frac{l^2} {9 \sqrt{3}} \left[ \sqrt{3} - \frac{4}{3} \pi \right]](7df1ffbaebc949122e7d06bd45d159ec.png) .
.
Второй интеграл:
Подстановка:
 .
.
Пределы интегрирования:
 .
.
Интеграл преобразуется к виду:

![= - \frac{1}{9 \sqrt{3}} \left[ \frac{v}{2} \sqrt{ \left(2l \right)^2 - v^2} + \frac{ \left(2l \right)^2}{2} \arcsin \left( \frac{v}{2l} \right) \right] \Bigg|^{-l}_{2l}=\frac{l^2} {9 \sqrt{3}} \left[ \frac {\sqrt{3}}{2} + \frac{4}{3} \pi \right]](a5b1da74bb03023fa0be9e8b1283cc35.png) .
.
Итак:
![\frac {1}{2}S_1 = \frac{l^2} {9 \sqrt{3}} \left[ \sqrt{3} - \frac{4}{3} \pi \right] + \frac{l^2} {9 \sqrt{3}} \left[ \frac {\sqrt{3}}{2} + \frac{4}{3} \pi \right]](0a474338f58659c6fc7613c724a71210.png) .
.
Площадь
 равна
равна .
.
- Площадь области между асимптотой и кривой равна площади петли
 .
.
Нахождение площади 
Площадь  , заключённая между ветвями кривой и асимптотой UV, вычисляется точно также, как и площадь
, заключённая между ветвями кривой и асимптотой UV, вычисляется точно также, как и площадь  ; интеграл берётся в пределах от 0 до
; интеграл берётся в пределах от 0 до  .
.
Этот интеграл вычисляется также, как и в предыдущем случае.
 , то есть, площади
, то есть, площади  и
и  равны между собой.
равны между собой.
- Объём тела, образованного при вращении дуги
 вокруг оси абсцисс
вокруг оси абсцисс 
Нахождение объёма вращения Объём (  ) тела, образованного при вращении дуги
) тела, образованного при вращении дуги  вокруг оси абсцисс, рассчитывается так:
вокруг оси абсцисс, рассчитывается так:


 .
.
Итак:
 .
.
Объём (
 ) тела, образованного при вращении одной ветви вокруг оси абсцисс, стремится к бесконечности. Этот объём вычисляется из предыдущего интеграла в пределах от
) тела, образованного при вращении одной ветви вокруг оси абсцисс, стремится к бесконечности. Этот объём вычисляется из предыдущего интеграла в пределах от  до
до  . Этот интеграл равен бесконечности, то есть
. Этот интеграл равен бесконечности, то есть .
.
Исследование кривой
При
 имеем
имеем  или
или  , или
, или  , то есть
, то есть  .
.Уравнение асимптоты UV определяется из выражения:
 .
.
Производная
Чтобы найти максимальное значение функции и уравнение касательной, вычислим производную функции:
 .
.
Приравниваем производную y' нулю и решаем, полученное уравнение, относительно x. Получим:
 . При этом значении x функция (2) имеет максимум на верхней дуге
. При этом значении x функция (2) имеет максимум на верхней дуге  — точка
— точка  и минимум на нижней дуге
и минимум на нижней дуге  — точка
— точка  . Значение функции в этих точках равно:
. Значение функции в этих точках равно: .
.
Значение производной y’ в точке
 равно
равно  , то есть касательные в точке
, то есть касательные в точке  взаимно перпендикулярны и наклонены к оси абсцисс под углом
взаимно перпендикулярны и наклонены к оси абсцисс под углом  .
.Ссылки

Декартов лист на Викискладе? - Д. К. Бобылёв Декартов лист // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
Категория:- Кривые
Wikimedia Foundation. 2010.