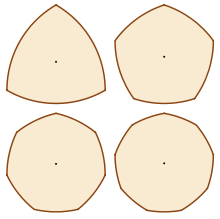
Кривая постоянной ширины

Примеры

Треугольник Рёло - кривая постоянной ширины. Стороны квадрата - опорные прямые: каждая сторона касается треугольника, но не пересекает его. Треугольник Рёло можно вращать, и при этом он всегда будет касаться каждой стороны квадрата; таким образом ширина треугольника (расстояние между двумя опорными прямыми) постоянна.

Кривая постоянной ширины $a$ — плоская выпуклая кривая, длина ортогональной проекции которой на любую прямую равна $a$.

Иными словами, кривой постоянной ширины называется плоская выпуклая кривая, расстояние между любыми двумя параллельными опорными прямыми которой постоянно и равно $a$ — «ширине» кривой.

Связанные определения

• Фигурой постоянной ширины называется фигура, граница которой является кривой постоянной ширины.

Примеры

Фигурами постоянной ширины являются:

• Круг;
• Треугольник Рёло;
• Многоугольник Рёло.

Свойства

• Длина кривой постоянной ширины $a$ равна $\pi a$ (теорема Барбье).
• Центры вписанной и описанной окружностей в кривую постоянной ширины совпадают, а сумма их радиусов равна ширине кривой.
• Фигура постоянной ширины $a$ может вращаться в квадрате со стороной $a$ всё время касаясь каждой из сторон.
• Среди всех фигур данной постоянной ширины треугольник Рёло имеет наименьшую площадь, а круг — наибольшую.
• Любую плоскую фигуру диаметра $a$ можно накрыть фигурой постоянной ширины $a$.

Применения

• Сверло, сделанное на основе треугольника Рёло, позволяет^[1] сверлить квадратные отверстия (с неточностью в 2 %).
• Британские монеты достоинством 20^[2] и 50 пенни имеют форму фигуры постоянной ширины, построенной на семиугольнике.
• Двигатель Ванкеля использует^[2] в качестве поршня вращающийся внутри камеры треугольник Рёло, что позволяет сразу получать вращательное движение.
• Грейферный механизм, отвечающий за «дискретную» протяжку ленты в кинопроекторе «Луч-2», использует вращающийся внутри подвижного квадрата треугольник Рёло^[2].

Вариации и обобщения

• Фигуры постоянной ширины можно определить как выпуклые фигуры способные вращаться внутри квадрата одновременно касаясь всех его сторон. Можно также рассматривать фигуры способные вращаться касаясь всех сторон некоторого $n$-угольника, например правильного $n$-угольника. Такие фигуры называются роторами^[3].
  • Например двуугольник образованный пересечением двух одинаковых кругов с углом при вершине равным $\pi/3$ является ротором равностороннего треугольника. Сверлом такой формы в принципе можно было бы сверлить треугольные отверстия без сглаженных углов.
• У фигур постоянной ширины существуют многомерные аналоги, смотри Тело постоянной ширины.

Примечания

1. ↑ «Сверление квадратных отверстий» / Математические этюды
2. ↑ ^{1 2 3} «Круглый треугольник Рело» / Математические этюды
3. ↑ Helmut Groemer, Geometric Applications of Fourier Series and Spherical Harmonics

Литература

• И. М. Яглом, В. Г. Болтянский, Выпуклые фигуры, выпуск 4 серии «Библиотека математического кружка» М.-Л., ГТТИ, 1951.-343 с.