- ГАМИЛЬТОНА ФУНКЦИЯ
- ГАМИЛЬТОНА ФУНКЦИЯ
-
(по имени ирл. математика У. Р. Гамильтона (W. R. Hamilton)), характеристич. функция механической системы, выраженная через канонические переменные: обобщённые координаты qi и обобщённые импульсы рi. Для системы со связями, явно не зависящими от времени t, движущейся в стационарном потенциальном силовом поле, Г. ф. H(qi, рi)=T+П, где П — потенц. энергия, а Т — кинетич. энергия системы, в выражении к-рой все обобщённые скорости qi заменены на Pi с помощью равенства рi=дТ/дqi. Т. о., в этом случае Г. ф. равна полной механич. энергии системы, выраженной через qi и pi. В общем случае Г. ф. H(pi, qi, t) может быть определена через др. характеристич. ф-цию — Лагранжа функцию L (qi, pi, t) равенством: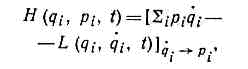
. в к-ром все qi должны быть также выражены через pi.Г. ф., как и ф-ция Лагранжа, полностью характеризует ту систему, для к-рой она определена, т. к., зная H(pi, qi, t), можно составить дифф. ур-ния движения системы (см. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕХАНИКИ).Г. ф. обобщается и на системы с бесконечным числом степеней свободы — классические физические поля. В этом случае роль обобщённых координат и импульсов играют значения ф-ции поля в каждой точке пр-ва и их производные по времени. Г. ф. системы взаимодействующих полей равна сумме Г. ф. свободных полей и энергии их вз-ствия. (Иногда в теории классич. полей Г. ф. наз. гамильтонианом, как и в теории квант. полей.)
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
.
