УСТОЙЧИВЫЕ РАСПРЕДЕЛЕНИЯ

УСТОЙЧИВЫЕ РАСПРЕДЕЛЕНИЯ

-распределения вероятностей, обладающих свойством, что для любых а₁>0, b₁, a₂ > 0, b₂ имеет место соотношение

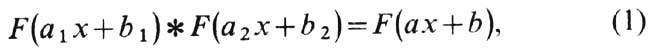
где а>0и b - нек-рые постоянные, F- ф-ция распределения У. р., * -символ операции свёртки двух ф-ций распределения.

Характеристич. ф-ция У. р.:

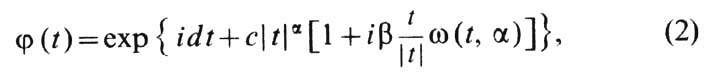
где 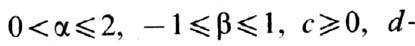-любое действительное число и

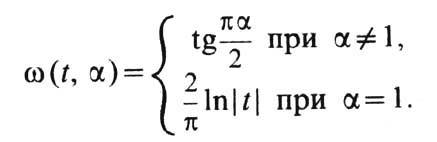
Число a наз. п о к а з а т е л е м у с т о й ч и в о г о р а с п р е-д е л е н и я. У. р. с показателем a = 2-Гаусса распределение, пример У. р. с показателем a= 1 - Коши распределение.

Благодаря (1) У. р. является безгранично делимым распределением (БДР), т. <е. может быть представлено как композиция (свёртка) любого числа п>=2одинаковых распределений. Для характеристич. ф-ции БДР имеет место т. <н. к а н о н и ч е с к о е п р е д с т а в л е н и е Л е в и:

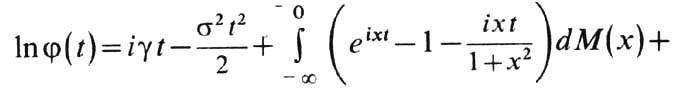
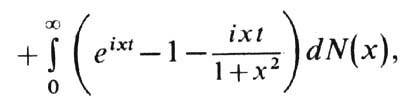
где характеристики представления g, s², M, N удовлетворяют условиям: 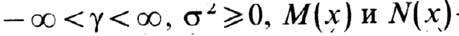-неубывающие непрерывные слева ф-ции на (-беск., 0) и (0, беск.) соответственно и такие, что

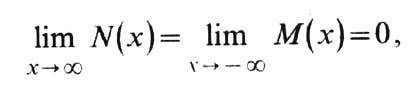
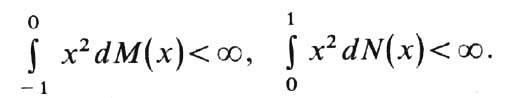
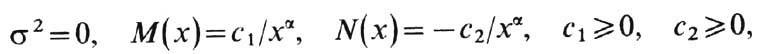
У. р. с показателем a, 0<a<2, соответствует канонич. представление Леви с характеристиками: 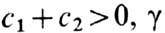-любое действительное число. Для У. р., за исключением вырожденного распределения, существуют плотности. Эти плотности бесконечно дифференцируемы, одновершинны и отличны от нуля или на всей прямой, или на полупрямой. Для У. р. с показателем a, 0<a<2, при d<a выполняются соотношения

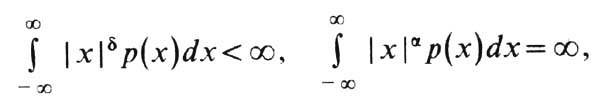
где р(х) - плотность У. р. Явный вид плотностей У. р. известен лишь в немногих случаях.

В совокупности У. р. выделяется к л а с с с т р о г о у ст о й ч и в ы х р а с п р е д е л е н и й, для к-рых имеет место равенство (1) при b₁ = b₂ = b =0. Характеристич. ф-ции строго устойчивого распределения с показателем 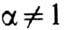даются ф-лой (2) при d=0. При a=1 строго устойчивым распределением является лишь распределение Коши. Спектрально положительные (отрицательные) У. р. характеризуются тем, что в канонич. представлении Леви М( х) = 0 (N( х) = 0). Для спектрально положительных У. р. существует преобразование Лапласа при Re s >= 0:

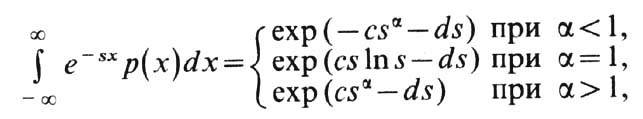
где р(х) - плотность спектрально положительного У. р. с показателем a, 0<a<2, c>0, d- действительное число, у многозначных ф-ций ln s,s^a выбираются те ветви, для к-рых ln s действительный, а s^a>0 при s>0.

У. р., как безгранично делимому распределению, соответствует однородный случайный процесс с независимыми приращениями (напр., Винеровский случайный процесс}. Стохастически непрерывный однородный случайный процесс с независимыми приращениями 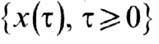наз. устойчивым, если приращение x(1) - x(0) имеет У . р.

Лит.:1) Гнеденко Б. В., Колмогоров А. Н., Предельные распределения для сумм независимых случайных величин, М.- Л., 1949; 2) Прохоров Ю. В., Розанов Ю. А., Теория вероятностей, 3 изд., М., 1987; 3) Ибрагимов И. А., Линник Ю. В., Независимые и стационарно связанные величины, М., 1965; 4) Скороход А. В., Случайные процессы с независимыми приращениями, М., 1964; 5) Золотарев В. М., Одномерные устойчивые распределения, М., 1983. Б. А. Рогозин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.