УСТОЙЧИВОСТЬ УПРУГИХ СИСТЕМ

УСТОЙЧИВОСТЬ УПРУГИХ СИСТЕМ

-свойство упругих систем возвращаться к состоянию равновесия после малых отклонений их из этого состояния. Понятие У. у. с. тесно связано с общими понятиями устойчивости движения и равновесия. Устойчивость является необходимым условием для любой конструкции. Потеря устойчивости может стать причиной разрушения как отд. элемента конструкции, так и сооружения в целом.

Нагрузка, при к-рой устойчивое равновесие переходит в неустойчивое, наз. критич. нагрузкой, а состояние системы- критич. состоянием. Установление критич. состояний составляет осн. предмет теории У. у. с.

Для прямого стержня, сжатого вдоль оси силой Р, значение критич. силы Р _кр определяется ф-лой Эйлера: 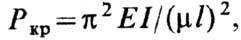где Е- модуль упругости материала; I- момент инерции поперечного сечения; l -длина стержня; m-коэф., зависящий от условий закрепления концов. В случае двух шарнирных опор, одна из к-рых неподвижна, а вторая подвижна, m=1

Для прямоуг. пластинки, сжатой в одном направлении, критич. напряжение 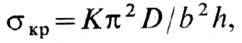где D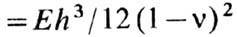 - т. <н. цилиндрич. жёсткость; b и h- ширина и толщина пластинки; v - коэф. Пуассона материала; К- коэф., зависящий от условий закрепления краёв и от отношения между размерами пластинки.

В случае круговой цилиндрич. оболочки, сжатой вдоль оси, можно установить т. н. верхнее критич. напряжение

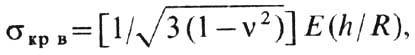
где h и R - толщина и радиус кривизны срединной поверхности оболочки. Несколько иную структуру имеют ф-лы для верхнего критич. напряжения при действии поперечного давления или скручивающих пар сил. Потеря устойчивости реальных оболочек во мн. случаях происходит при меньшей нагрузке вследствие значит. влияния разл. факторов, особенно нач. неправильностей формы.

Для сложных конструкций точное решение задачи У. у. с. затруднено, поэтому прибегают к разл. приближённым методам. Для многих из них пользуются энергетич. критерием устойчивости, в к-ром рассматривается характер изменения потенц. энергии П системы при малом отклонении её от положения равновесия (для устойчивого равновесия П = min). При рассмотрении неконсервативных систем, напр. стержня, сжатого силой, наклон к-рой меняется в процессе изгиба (следящая сила), применяется дина-мич. критерий, заключающийся в определении малых колебаний нагруженной системы.

Важное значение имеет исследование т. н. закритич. поведения упругих систем. Оно требует решения нелинейных краевых задач. Для стержня закритич. деформация оказывается возможной лишь при его очень большой гибкости. Напротив, для тонких пластинок вполне возможны значит. прогибы в закритич. стадии-при условии, что края пластинки подкреплены жёсткими стержнями (стрингерами). Для оболочек закритич. деформация связана обычно с про-щёлкиванием и потерей несущей способности конструкции.

Приведённые выше данные относятся к случаю, когда потеря У. у. с. имеет место в пределах упругости материала. Для исследования У. у. с. за пределами упругости пользуются пластичности теорией. Если нагрузка, приводящая к потере устойчивости, динамическая, необходимо учитывать силы инерции элементов конструкции, отвечающие характерным перемещениям. При ударных нагрузках исследуются волновые процессы передачи усилий в конструкции. Если материал конструкции находится в состоянии ползучести, для определения критич. параметров пользуются соотношениями теории ползучести.

Лит.: Болотин В. В., Динамическая устойчивость упругих систем, М., 1956; его же, Неконсервативные задачи теории упругой устойчивости, М., 1961; Вольмир А. С., Устойчивость деформируемых систем, 2 изд., М., 1967; его же, Оболочки в потоке жидкости и газа. Задачи гидроупругости, М., 1979; Тимошенко С. П., Устойчивость стержней, пластин и оболочек, М., 1971.

А. С. Вольмир.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.