- ВЕРОЯТНОСТЕЙ ТЕОРИЯ
- ВЕРОЯТНОСТЕЙ ТЕОРИЯ
-
- раздел математики, в к-ром строят и изучают матем. модели случайных явлении.
Случайность присуща в той или иной степени подавляющему большинству протекающих в природе процессов. Обычно она присутствует там, где существ. влияние на ход процесса оказывает очень большое число незначительных по отдельности факторов (как, напр., при движении броуновской частицы или в классич. примере с бросанием монеты), особенно в том случае, когда система динамически неустойчива; статистич. характер имеют также законы квантовой механики. Внешне случайность проявляется как недостаточная регулярность в массовых явлениях, к-рая не позволяет с достоверностью предсказывать наступление определ. событий, т. е. не допускает описания этих явлений в рамках детерминиров. моделей. Тем не менее при изучении таких явлений выявляются определ. закономерности. Свойственная случайным событиям нерегулярность, как правило, компенсируется наличием т. н. статистич. закономерности, стабилизации частот наступлений случайных событий в длинном ряду испытаний; тогда говорят, что данные случайные события имеют определ. вероятность Пусть при каждом осуществлении нек-рого воспроизводимого комплекса условий С может наступать или не наступать событие А. Наличие у события А при условиях С определ. вероятности р означает, что в достаточно длинной серии испытаний (повторных осуществлений условий С; предполагается, что эти испытания в нек-ром смысле независимы) частота наступления события А, т. <е. отношение числа тех испытаний из серии, в к-рых А наступило, к общему их числу, приблизительно равна p.T. о., для описания связи случайных событий с условиями их наступления вместо обычного для классич. естествознания утверждения "в условиях С наступает событие А" приходится ограничиваться утверждением "при условиях С событие А имеет вероятность р". Именно для таких случайных событий, имеющих определ. вероятность, удалось построить содержат. матем. теорию, к-рая и носит название В. т. На практике особенно часто используют такие её результаты, к-рые позволяют утверждать, что вероятность P(А )наступления определ. события А близка к 1, т. е. что А практически достоверно. Такие результаты относятся, как правило, к области предельных теорем В. т., к-рые и являются её осн. содержанием.
Статистич. закономерности были известны давно, понятия В. т. возникли в сер. 17 в. в работах Б. Паскаля (В. Pascal), П. Ферма (P. Fermat) и X. Гюйгенса (Ch. Huygens), Существ. вклад в развитие В. т. внесли Я. Бернулли (J. Bernoulli), П. Лаплас (P. Laplace), К. Гаусс (С. Gauss), C. Пуассон (S. Poisson), П. Л. Чебышев. В кон. 19 - нач. 20 вв. открыто большое кол-во статистич. закономерностей в физике, биологии и др. науках (радиоакт. распад, законы Менделя и т. д.). Следует отметить, что статистич. закономерности возникают и в неслучайных схемах (напр., в распределении цифр в таблицах ф-ций и т. п.); это обстоятельство используется при "моделировании" (имитации) случайных явлений, напр. в Монте-Карло методе.
Основные понятия теории вероятностей. Для вероятностей случайных событий справедливы след. простые соотношения. Пусть А и В - события, относящиеся к условиям С. Обозначим через А
 В объединение событий А и В (событие "наступает А или В"), а через
В объединение событий А и В (событие "наступает А или В"), а через  - достоверное событие, т. е. событие, наступающее при каждом осуществлении условий С. События Au B наз. несовместными, если их одноврем. наступление невозможно. Из частотной интерпретации вероятности следует:
- достоверное событие, т. е. событие, наступающее при каждом осуществлении условий С. События Au B наз. несовместными, если их одноврем. наступление невозможно. Из частотной интерпретации вероятности следует:

для несовместных А и В. Последнее свойство обобщается и на любое конечное число попарно несовместных событий; это свойство наз. теоремой сложения вероятностей.
Строгую В. т. можно построить, исходя лишь из этих соотношений. В наиб. простом её варианте (элементарной В. т.) предполагают, что испытание заканчивается одним из конечного набора
 исходов
исходов  , к-рые наз. элементарными событиями. Каждому исходу
, к-рые наз. элементарными событиями. Каждому исходу  приписывают вероятность
приписывают вероятность  О, причём
О, причём  . Рассматриваемые в элементарной В. т. события
. Рассматриваемые в элементарной В. т. события  имеют вид "наступает
имеют вид "наступает  , или
, или  , ..., или
, ..., или  "; исходы
"; исходы  наз. благоприятствующими А . Событие
наз. благоприятствующими А . Событие  наз. достоверным. Вероятность P (А )события А равна сумме вероятностей благоприятствующих ему исходов:
наз. достоверным. Вероятность P (А )события А равна сумме вероятностей благоприятствующих ему исходов:  . Именно так устроена любая числовая ф-ция, заданная на классе всех подмножеств
. Именно так устроена любая числовая ф-ция, заданная на классе всех подмножеств  и удовлетворяющая условиям (1-3) (при этом
и удовлетворяющая условиям (1-3) (при этом  определяют как объединение наборов благоприятствующих А и В исходов, а несовместными наз. события, не имеющие общих благоприятствующих исходов).
определяют как объединение наборов благоприятствующих А и В исходов, а несовместными наз. события, не имеющие общих благоприятствующих исходов).
В. т. развивалась вначале в рамках частного случая элементарной В. т., в к-ром
 и, следовательно, вероятность события А равна отношению числа благоприятствующих А исходов к общему числу N"равновозможных" исходов (т. н. классическое определение вероятности; именно оно имеется в виду, когда говорят о случайном выборе одного из нек-рой совокупности предметов). Такое определение вероятности является, по существу, спец. формой записи симметрии случайного явления и поэтому часто встречается при использовании дискретных вероятностных моделей (напр., в статистич. физике, биологии и т. п.). Вычисление вероятностей при этом сводится к подсчёту числа благоприятствующих исходов, т. е. к комбинаторной задаче.
и, следовательно, вероятность события А равна отношению числа благоприятствующих А исходов к общему числу N"равновозможных" исходов (т. н. классическое определение вероятности; именно оно имеется в виду, когда говорят о случайном выборе одного из нек-рой совокупности предметов). Такое определение вероятности является, по существу, спец. формой записи симметрии случайного явления и поэтому часто встречается при использовании дискретных вероятностных моделей (напр., в статистич. физике, биологии и т. п.). Вычисление вероятностей при этом сводится к подсчёту числа благоприятствующих исходов, т. е. к комбинаторной задаче.
В рамках элементарной В. т. можно также наиб. просто определить осн. понятия В. т. Совмещением (или пересечением) событий А и В наз. событие
 = "наступает и А и В" (т. е. набор благоприятствующих ему исходов равен пересечению множеств исходов, благоприятствующих А и В). Все эти определения обобщаются и на любое конечное число событий. Наряду с символами
= "наступает и А и В" (т. е. набор благоприятствующих ему исходов равен пересечению множеств исходов, благоприятствующих А и В). Все эти определения обобщаются и на любое конечное число событий. Наряду с символами  ,
,  в В. т. широко используют и др. теоретико-множеств. обозначения (что естественно, поскольку события в ней отождествляются с множествами исходов). Так,
в В. т. широко используют и др. теоретико-множеств. обозначения (что естественно, поскольку события в ней отождествляются с множествами исходов). Так,  -дополнительное (или противоположное) к А событие (образованное всеми неблагоприятствующими А исходами); запись
-дополнительное (или противоположное) к А событие (образованное всеми неблагоприятствующими А исходами); запись  означает, что появление события А влечёт наступление В. Приведём простейшие свойства вероятности [все они вытекают из 1)-3)]: 4)
означает, что появление события А влечёт наступление В. Приведём простейшие свойства вероятности [все они вытекают из 1)-3)]: 4)  ; 5) если
; 5) если  , то
, то  ; 6)
; 6)
 [значит, для произвольных А и В в 3) вместо равенства должен стоять знак
[значит, для произвольных А и В в 3) вместо равенства должен стоять знак  ].
].
Условная вероятность события А при условии В определяется как
 , т. е. вероятность события А на подмножестве тех событий, где выполнено В. Такое определение хорошо согласуется с частотной интерпретацией вероятностей. На практике часто используют след. соотношения между вероятностями случайных событий. Пусть B1, ..., Bn- , попарно несовместные события и их объединение есть достоверное событие W. Формула полной вероятности
, т. е. вероятность события А на подмножестве тех событий, где выполнено В. Такое определение хорошо согласуется с частотной интерпретацией вероятностей. На практике часто используют след. соотношения между вероятностями случайных событий. Пусть B1, ..., Bn- , попарно несовместные события и их объединение есть достоверное событие W. Формула полной вероятности

для любого события А позволяет вычислить его вероятность по условным вероятностям
 , найти к-рые часто значительно легче, чем P(A), Формулу Бейеса
, найти к-рые часто значительно легче, чем P(A), Формулу Бейеса  широко используют в статистике, события
широко используют в статистике, события  при этом наз. гипотезами, P(B1)- их априорными вероятностями, а
при этом наз. гипотезами, P(B1)- их априорными вероятностями, а  -апостериорной вероятностью
-апостериорной вероятностью  (вероятность справедливости гипотезы Bj, если известно, что наступило событие А).
(вероятность справедливости гипотезы Bj, если известно, что наступило событие А).
События A и B наз. независимыми, если условная вероятность одного из них при условии наступления другого равна его безусловной вероятности, или, что то же, если
 . Аналогично события A1, А 2, ..., An наз. независимыми, если для любых
. Аналогично события A1, А 2, ..., An наз. независимыми, если для любых 

(Отметим, что из попарной независимости событий отнюдь не вытекает их независимость в совокупности.) Последнее равенство наз. теоремой умножения вероятностей. Ф-ла (1) останется справедливой, если нек-рые из Ai заменить в обеих частях на дополнительные к ним события

Пример. Пусть события А 1, ..., An независимы и имеют каждое вероятность р. Эти события можно интерпретировать как "успехи" в наблюдении нек-рого случайного события в п независимых испытаниях. Тогда вероятность наступления ровно m успехов равна

Действительно, можно взять
 , все ik=0 или 1}, где ik=l соответствует наступлению А k, а ik=0 - его ненаступлению. Наступлению т успехов благоприятствуют те исходы (i1, ..., in), у к-рых среди ik ровно т единиц; всего таких исходов
, все ik=0 или 1}, где ik=l соответствует наступлению А k, а ik=0 - его ненаступлению. Наступлению т успехов благоприятствуют те исходы (i1, ..., in), у к-рых среди ik ровно т единиц; всего таких исходов  , а вероятность каждого такого исхода в силу независимости Ak, свойства (4) и ф-лы (1) равна
, а вероятность каждого такого исхода в силу независимости Ak, свойства (4) и ф-лы (1) равна 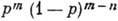 .
.
К этому примеру непосредственно примыкает одна из первых (и важнейших) предельных теорем В. т.- теорема Бернулли (простейшая форма больших чисел закона), согласно к-рой вероятность значит. уклонения частоты успехов v от вероятности р при больших п становится сколь угодно малой. Т. <о., рассматриваемая матем. модель случайных явлений приводит к согласующемуся с практич. наблюдениями выводу о стабилизации частот случайных событий около их вероятностей.
Скорость стремления частоты nк p оценивают с помощью теоремы Лапласа (частный случай центральной предельной теоремы). С ростом n вероятность
 стремится к Ф(b)-Ф(а), где -
стремится к Ф(b)-Ф(а), где -  ф-ция стандартного нормального распределения ( Гаусса распределения).
ф-ция стандартного нормального распределения ( Гаусса распределения).
Частота n является типичным примером др. объекта В. <т.- случайной величины. Так называется любая ф-ция X, ставящая в соответствие каждому исходу
 число xi, при этом среди xi могут быть и равные. Конкретный вид отображения
число xi, при этом среди xi могут быть и равные. Конкретный вид отображения  часто несуществен, достаточно знать лишь распределение случайной величины X, т. е. набор разл. возможных значений
часто несуществен, достаточно знать лишь распределение случайной величины X, т. е. набор разл. возможных значений  и приписываемых им вероятностей. Математическое ожидание случайной величины X определяется как число
и приписываемых им вероятностей. Математическое ожидание случайной величины X определяется как число 
Пример. Пусть в предыдущем примере
 для исхода (i1, ..., ik, ..., ii), k=1, ..., n, т. е. случайные величины
для исхода (i1, ..., ik, ..., ii), k=1, ..., n, т. е. случайные величины  принимают на N= 2n исходах лишь два возможных значения: 0 и 1, с вероятностями 1- р и р соответственно, так что
принимают на N= 2n исходах лишь два возможных значения: 0 и 1, с вероятностями 1- р и р соответственно, так что 
Частота успехов
 , при этом
, при этом  равна (2), т. е. nn имеет биномиальное распределение.
равна (2), т. е. nn имеет биномиальное распределение.
В этом примере рассматривался набор случайных величин X=(X1, ..., Xn), или случайный вектор. Основной характеристикой случайного вектора, как и случайной величины, является его распределение (совместное распределение случайных величин X1, ..., Xn), т. е. набор возможных его значений (x1, ..., х п )и их вероятностей, равных вероятностям совмещений событий
 . Если эти события для всех наборов (x1, ..., xn) оказываются независимыми, то случайные величины X1, ..., Xn также наз. независимыми. О важнейших числовых характеристиках случайных величин см. Дисперсия, Моменты случайной величины, Корреляции коэффициент.
. Если эти события для всех наборов (x1, ..., xn) оказываются независимыми, то случайные величины X1, ..., Xn также наз. независимыми. О важнейших числовых характеристиках случайных величин см. Дисперсия, Моменты случайной величины, Корреляции коэффициент.
Аксиоматика теории вероятностей. Элементарная В. т. недостаточна для описания случайных явлений уже в простых ситуациях. Модель с конечным числом исходов непригодна, напр., для понятия "случайно выбранной на отрезке точки". Такого рода трудности позволяет преодолеть схема, предложенная A. H. Колмогоровым в 1933 и ставшая с тех пор общепринятой.
Осн. эле. <ментами этой аксиоматич. схемы являются: пространство элементарных событий
 , к-рое может быть множеством произвольной природы, нек-рый класс
, к-рое может быть множеством произвольной природы, нек-рый класс  его подмножеств, т. е. множеств элементарных событий, к-рые наз. событиями, и числовая ф-ция P на
его подмножеств, т. е. множеств элементарных событий, к-рые наз. событиями, и числовая ф-ция P на  , к-рая удовлетворяет условиям 1)-3) и наз. вероятностью. Для корректности матем. модели требуют, чтобы класс
, к-рая удовлетворяет условиям 1)-3) и наз. вероятностью. Для корректности матем. модели требуют, чтобы класс  был s-алгеброй (т. е. чтобы сам
был s-алгеброй (т. е. чтобы сам  было событием и, значит, принадлежало
было событием и, значит, принадлежало  , чтобы наряду с любым событием А классу
, чтобы наряду с любым событием А классу  принадлежало бы и его дополнение
принадлежало бы и его дополнение  и чтобы для любой бесконечной последовательности событий A1, A2, ... их объединение
и чтобы для любой бесконечной последовательности событий A1, A2, ... их объединение  также было событием), а ф-ция P была счётно-аддитивной, т. е. чтобы вместе со свойством 3) имело место следующее: если события A1, A2, ... попарно несовместны, то
также было событием), а ф-ция P была счётно-аддитивной, т. е. чтобы вместе со свойством 3) имело место следующее: если события A1, A2, ... попарно несовместны, то 
 [это означает, что P является мерой на измеримом пространстве
[это означает, что P является мерой на измеримом пространстве  ]. Тройка
]. Тройка  наз. вероятностным пространством. Очевидно, что элементарная В. т. является на самом деле частным случаем реализации этой схемы; её осн. определения остаются в силе и в общем случае. Одно из существ. отличий заключается в определении случайной величины
наз. вероятностным пространством. Очевидно, что элементарная В. т. является на самом деле частным случаем реализации этой схемы; её осн. определения остаются в силе и в общем случае. Одно из существ. отличий заключается в определении случайной величины  : требуют, чтобы множества
: требуют, чтобы множества  принадлежали классу
принадлежали классу  при всех x. Для таких ф-ций X можно определить абстрактный интеграл Лебега, к-рый и наз. матем. ожиданием случайной величины X. Задавать случайную величину X удобнее всего с помощью её ф-ции распределения
при всех x. Для таких ф-ций X можно определить абстрактный интеграл Лебега, к-рый и наз. матем. ожиданием случайной величины X. Задавать случайную величину X удобнее всего с помощью её ф-ции распределения 
Предельные теоремы. Осн. задача В. т.- находить по вероятностям одних случайных событий вероятности других, связанных к.-л. образом с первыми. Типичный пример-определение вероятности события

 , где Xk - независимые случайные величины, имеющие одно и то же известное распределение. Однако при больших п непосредств. вычисление вероятности P(An )становится очень трудоёмким и практически невозможным. В таких случаях полезны предельные теоремы В. т., к-рые позволяют найти приближённые значения искомых вероятностей. Так, если в нашем примере матем. ожидание
, где Xk - независимые случайные величины, имеющие одно и то же известное распределение. Однако при больших п непосредств. вычисление вероятности P(An )становится очень трудоёмким и практически невозможным. В таких случаях полезны предельные теоремы В. т., к-рые позволяют найти приближённые значения искомых вероятностей. Так, если в нашем примере матем. ожидание
 , то в силу закона больших
, то в силу закона больших
чисел при любых а< р < b вероятность P (An )с ростом п стремится к 1. Центральная предельная теорема уточняет этот результат: если дисперсия
 конечна, то случайная величина
конечна, то случайная величина  имеет приблизительно нормальное распределение со средним р и дисперсией
имеет приблизительно нормальное распределение со средним р и дисперсией  , т. е. при
, т. е. при 
 ,
,  и а<b вероятность события An стремится с ростом п к Ф (b) - Ф ( а). Т. о., для сходимости распределения случайной величины
и а<b вероятность события An стремится с ростом п к Ф (b) - Ф ( а). Т. о., для сходимости распределения случайной величины  к нормальному достаточно лишь наличия у слагаемых Xk конечной дисперсии, а в остальном вид распределения Xk не важен; этим объясняется широта распространения нормального распределения в практич. применениях В. т. Не менее естеств. образом при суммировании случайных величин с бесконечной дисперсией в качестве предельных распределений появляются устойчивые распределения, отличные от нормального (напр., Коши распределение). На практике весьма полезны и т. н. теоремы о больших отклонениях, к-рые позволяют с высокой относит. точностью аппроксимировать малые вероятности. Осн. метод доказательства предельных теорем основан на использовании характеристических функций. Аналогичные предельные теоремы доказаны и для случайных векторов (в т. ч. бесконечномерных), известны также предельные теоремы для объектов более общей алгебраич. природы: случайных матриц, элементов группы и т. д. Кроме того, можно ослабить условие независимости
к нормальному достаточно лишь наличия у слагаемых Xk конечной дисперсии, а в остальном вид распределения Xk не важен; этим объясняется широта распространения нормального распределения в практич. применениях В. т. Не менее естеств. образом при суммировании случайных величин с бесконечной дисперсией в качестве предельных распределений появляются устойчивые распределения, отличные от нормального (напр., Коши распределение). На практике весьма полезны и т. н. теоремы о больших отклонениях, к-рые позволяют с высокой относит. точностью аппроксимировать малые вероятности. Осн. метод доказательства предельных теорем основан на использовании характеристических функций. Аналогичные предельные теоремы доказаны и для случайных векторов (в т. ч. бесконечномерных), известны также предельные теоремы для объектов более общей алгебраич. природы: случайных матриц, элементов группы и т. д. Кроме того, можно ослабить условие независимости 
Случайные процессы. Одним из осн. разделов В. т. является теория случайных процессов и полей, важность к-рой обусловлена огромным кол-вом её приложений. Случайным процессом наз. однопараметрич. семейство случайных величин X(t).B большинстве приложений параметр t является временем, и термин "случайный процесс" относится именно к этому случаю; когда одномерный параметр t не имеет смысла времени, часто говорят о случайной функции, а в случае многомерного t - о случайном поле. Если параметр t целочисленный, то случайный процесс наз. случайной последовательностью или временным рядом. Случайный процесс, как и случайную величину, можно охарактеризовать его распределением; для этого достаточно задать его конечномерные распределения, т. е. совокупность совместных распределений случайных величин
 для всевозможных
для всевозможных  и п. Для случайных процессов, как и для случайных величин, доказано большое кол-во предельных теорем (иногда их наз. функциональными предельными теоремами).
и п. Для случайных процессов, как и для случайных величин, доказано большое кол-во предельных теорем (иногда их наз. функциональными предельными теоремами).
Наиб. развита теория двух спец. классов случайных процессов, к-рые в то же время чаще всего встречаются в применениях: марковских случайных процессов и стационарных случайных процессов. Случайный процесс наз. марковским (или процессом без последействия), если для любых
 условное распределение X (t2 )при условии, что известно поведение X (t )при
условное распределение X (t2 )при условии, что известно поведение X (t )при  , зависит только от значения X(t1) (т. е. "будущее" при фиксиров. "настоящем" от "прошлого" не зависит). Такие процессы являются естеств. обобщением детерминиров. процессов, рассматриваемых, напр., в классич. механике, для к-рых состояния системы в моменты времени
, зависит только от значения X(t1) (т. е. "будущее" при фиксиров. "настоящем" от "прошлого" не зависит). Такие процессы являются естеств. обобщением детерминиров. процессов, рассматриваемых, напр., в классич. механике, для к-рых состояния системы в моменты времени  однозначно определяются её состоянием в момент t1; мн. задачи для марковских процессов сводятся к дифференц. ур-ниям для ф-ций, определяющих распределения вероятностей процессов.
однозначно определяются её состоянием в момент t1; мн. задачи для марковских процессов сводятся к дифференц. ур-ниям для ф-ций, определяющих распределения вероятностей процессов.
Стационарность случайного процесса означает неизменность во времени его вероятностных закономерностей. В В. т. рассматривают два вида стационарности: стационарность в узком смысле, когда конечномерные распределения инвариантны относительно сдвига времени, и стационарность в широком смысле, когда от времени t не зависят лишь матем. ожидания
 и
и  . На практике чаще используют предположение о стационарности в широком смысле.
. На практике чаще используют предположение о стационарности в широком смысле.
Важнейшей областью применения результатов В. т. и источником новых задач для неё является математическая статистика - раздел математики, посвящённый матем. методам обработки и использования статистич. данных. Типичными для матем. статистики являются задачи, в известном смысле обратные задачам В. т.: если в последней, напр., требуется, зная "природу" случайного явления (распределение соотв. вероятностей), указать, как будут себя вести наблюдаемые в эксперименте характеристики этого явления, то в матем. статистике, наоборот, требуется по эксперим. данным сделать выводы о природе случайного явления. Осн. задачами матем. статистики являются статистическое оценивание и проверка статистических гипотез.
Лит.: Гнеденко Б. В., Курс теории вероятностей, 5 изд., M., 1969; Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., т. 1-2, [3 изд.], M., 1984; Смирнов H. В., Дунин Барковский И. В., Курс теории вероятностей и математической статистики для технических приложений, 3 изд., M., 1969; Прохоров Ю. В., Розанов Ю. А., Теория вероятностей, 2 изд., M., 1973; Боровков А. А., Теория вероятностей, M., 1976.
К. А. Боровков.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
