- ПЕРЕСТАНОВОЧНЫЕ СООТНОШЕНИЯ
- ПЕРЕСТАНОВОЧНЫЕ СООТНОШЕНИЯ
-
(коммутационные соотношения), фундаментальные соотношения в квант. теории, устанавливающие связь между последоват. действиями на волновую функцию (пли вектор состояния) двух операторов (L^1 и L^2), расположенных в разном порядке (т. е. L^1L^2 и L^2L^1). П. с. определяют алгебру операторов (q-чисел). Если два оператора переставимы (коммутируют), т. е. L^1L^2=L^2L^1, то соответствующие им физ. величины L1 и L2 могут иметь одновременно определённые значения. Если же их действие в разном порядке отличается числовым фактором (с), т. е. L^iL^2-L^2L^l=c, то между соответствующими физ. величинами имеет место неопределённостей соотношение DL1DL2?1/2?c?, где DL1 и DL2 — неопределённости (дисперсии) измеряемых значений физ. величин L1 и L2. Важнейшими в квант. механике явл. П. с. между операторами обобщённой координата q^ и сопряжённого ей обобщённого импульса р^, q^p^-p^q^=iћ. Если оператор L^ не зависит от времени явно и переставим с гамильтонианом системы Н^, 1. е. L^H^=H^L^, то физ. величина L (а также её ср. значение, дисперсия и т. д.) сохраняет своё значение во времени.В квант. механике систем тождеств. ч-ц и квант. теории поля фундам. значение имеют П. с. для операторов рождения (а+) и поглощения (а-) ч-ц. Для системы свободных (невзаимодействующих) бозонов оператор рождения ч-цы в состоянии n, а+n и оператор поглощения такой ч-цы an-удовлетворяют П. с. а-n а+n- а+nа-n=1, а для фермионое. a-na+n+a+n a-n=1; последнее П. с. явл. формальным выражением Паули принципа.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ПЕРЕСТАНОВОЧНЫЕ СООТНОШЕНИЯ
-
- алгебраич. равенства, к-рым подчинены коммутаторы или антикоммутаторынек-рых матем. величин, в частности величин, встречающихся при формулировкеквантовой теории, напр. операторов квантовой механики. Если А 1 и А 2 - две такие величины, то коммутатором [A1,А2] наз. разность между произведениями A1A2 и А2 А1, т. е. [ А1, А2]= А1 А2 - A2Al. Антикоммутатором{ А1, А2} наз. сумма этих произведений, <т. е. { А1, А2} = А1, А2+ А2 А1. Обычно коммутаторыили антикоммутаторы нек-рой совокупности величин А1, А2,..., А п выражаются посредством П. <с. через линейные комбинации тех же величин. Важнейшие свойства (напр.,допустимые значения) физ. величин А1,...,А п определяютсяименно П. с. и не зависят от представления последних, т. е. от того, какимконкретным способом реализованы величины А1...., А п. Этим объясняется фундам. роль П. с. в квантовой физике.
Если П. с. не включают антикоммутаторов, <т. е. имеют вид [ А j, А k] =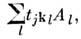 то П. с. задают нек-рую Ли алгебру, причём числа tjkl наз. <структурными константами соответствующей Ли группы, а величины А1,...,А п- генераторами этой группы. Реализация генераторов А1...,А п самосопряжёнными операторами в гильбертовом пространстве иликонечномерном евклидовом пространстве наз. представлением алгебры Ли. Приведёмнек-рые примеры.
то П. с. задают нек-рую Ли алгебру, причём числа tjkl наз. <структурными константами соответствующей Ли группы, а величины А1,...,А п- генераторами этой группы. Реализация генераторов А1...,А п самосопряжёнными операторами в гильбертовом пространстве иликонечномерном евклидовом пространстве наз. представлением алгебры Ли. Приведёмнек-рые примеры.
Если все tjkl=0, т. е. если все попарные коммутаторы равны нулю, то соответствующаягруппа наз. абелевой или коммутативной. Тогда в каждом представлении можноодновременно привести генераторы А1, ..., А п кдиагональному виду. Физически это означает, что величины А1...., А п могут иметь одновременно точные значения. Если в числегенераторов есть гамильтониан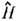 квантовойсистемы, то в состояниях с фиксиров. энергией
квантовойсистемы, то в состояниях с фиксиров. энергией 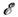 все др. физ. величины из числа генераторов А1,..., А п также могут принимать вполне определ. значения. Поскольку гамильтониануправляет временной эволюцией системы, все величины А1,..., А п оказываются интегралами движения, т. е. сохраняютсяс течением времени. Так, в задаче о движении частицы в центр. поле попарноперестановочными являются гамильтониан
все др. физ. величины из числа генераторов А1,..., А п также могут принимать вполне определ. значения. Поскольку гамильтониануправляет временной эволюцией системы, все величины А1,..., А п оказываются интегралами движения, т. е. сохраняютсяс течением времени. Так, в задаче о движении частицы в центр. поле попарноперестановочными являются гамильтониан 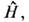 оператор квадрата момента импульса
оператор квадрата момента импульса 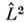 иоператор
иоператор 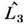 проекции момента импульса на к.-л. ось. Поэтому в пространстве состоянийсуществует базис, составленный из собств. векторов сразу трёх операторов:
проекции момента импульса на к.-л. ось. Поэтому в пространстве состоянийсуществует базис, составленный из собств. векторов сразу трёх операторов: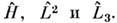 Это позволяет использовать стандартную классификацию состояний частицыс помощью трёх квантовых чисел - главного п, орбитального (азимутального). и магнитного m.
Это позволяет использовать стандартную классификацию состояний частицыс помощью трёх квантовых чисел - главного п, орбитального (азимутального). и магнитного m.
Если n = 3, а А1=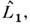 А 2 =
А 2 =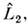 А 3 =
А 3 =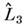 - проекции операторов момента импульса на оси х, у,z, то П. <с. приобретают форму
- проекции операторов момента импульса на оси х, у,z, то П. <с. приобретают форму 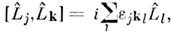 где
где 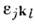 -полностью антисимметричный тензор. В этом случае П. с. задают простейшуюнеабелеву алгебру - алгебру Ли группы SU2. Группа SU2 возникает в физике всегда, когда физ. система обладает симметрией поотношению к вращениям трёхмерного пространства. Из П. с. видно, что разл. <проекции момента не перестановочны друг с другом, так что они не имеютодновременно точных значений. К диагональному виду можно привести любой, <но только один из трёх операторов, напр.
-полностью антисимметричный тензор. В этом случае П. с. задают простейшуюнеабелеву алгебру - алгебру Ли группы SU2. Группа SU2 возникает в физике всегда, когда физ. система обладает симметрией поотношению к вращениям трёхмерного пространства. Из П. с. видно, что разл. <проекции момента не перестановочны друг с другом, так что они не имеютодновременно точных значений. К диагональному виду можно привести любой, <но только один из трёх операторов, напр.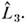 Его собств. значения дискретны и равны
Его собств. значения дискретны и равны 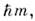 где т - целое или полуцелое число. Квадрат оператора момента
где т - целое или полуцелое число. Квадрат оператора момента 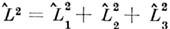 также имеет лишь дискретные собств. значения
также имеет лишь дискретные собств. значения 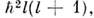 где l - целое или полуцелое неотрицат. число. При заданном l имеем т = l, l -1, ..., - l. Если l целое, то l и т и являются упомянутыми орбитальным и магнитным квантовыми числами.
где l - целое или полуцелое неотрицат. число. При заданном l имеем т = l, l -1, ..., - l. Если l целое, то l и т и являются упомянутыми орбитальным и магнитным квантовыми числами.
Если п =8, а П. с. имеют ту жеформу [ Аj, Аk] =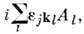 но j,k,l =1,2,...,8, то П. с. определяют алгебру Ли группы SU3. Еёгенераторы порождают, напр., "вращения" в пространстве цветов кварка. Поотношению к таким вращениям симметричен гамильтониан квантовой хромодинамики- теории, описывающей сильное взаимодействие элементарных частиц. Физ. <состояния квантовой хромодинамики должны быть "бесцветными", т. е. принадлежатьодномерным (синглетным) представлениям группы SU3.
но j,k,l =1,2,...,8, то П. с. определяют алгебру Ли группы SU3. Еёгенераторы порождают, напр., "вращения" в пространстве цветов кварка. Поотношению к таким вращениям симметричен гамильтониан квантовой хромодинамики- теории, описывающей сильное взаимодействие элементарных частиц. Физ. <состояния квантовой хромодинамики должны быть "бесцветными", т. е. принадлежатьодномерным (синглетным) представлениям группы SU3.
Пусть п = 3, a A1=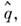 A2=
A2=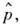 А3=
А3=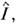 где
где 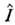 -единичный оператор, а
-единичный оператор, а 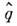 и
и 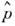 - операторы координаты и импульса частицы. Равенство
- операторы координаты и импульса частицы. Равенство 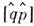 =
=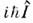 задаётт. н. канонические П. с. для системы с одной степенью свободы. Они определяюталгебру Ли группы Гейзенберга. Из них видно, что координата и импульс немогут принимать одновременно определ. значения. Если
задаётт. н. канонические П. с. для системы с одной степенью свободы. Они определяюталгебру Ли группы Гейзенберга. Из них видно, что координата и импульс немогут принимать одновременно определ. значения. Если 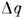 и
и 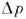 - неопределённостив значениях координаты и импульса, то
- неопределённостив значениях координаты и импульса, то 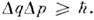 Это - частный случай неопределённостей соотношения. Для системыс т степенями свободы, т. е. для системы, гамильтониан к-рой зависитот т операторов обобщённых координат
Это - частный случай неопределённостей соотношения. Для системыс т степенями свободы, т. е. для системы, гамильтониан к-рой зависитот т операторов обобщённых координат 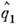 ,....
,....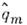 и от . сопряжённыхэтим координатам импульсов
и от . сопряжённыхэтим координатам импульсов 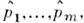 канонич. П. с. имеют вид
канонич. П. с. имеют вид 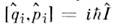 (здесь выписаны только ненулевые коммутаторы). Вообще, переход от классическогок квантовому описанию физ. системы можно трактовать как замену классических Пуассонаскобок коммутаторами операторов соответствующих величин. Из канонич. <П. с. следует, что каждая пара канонич. переменных qi,pi удовлетворяетсоотношению неопределённостей. В представлении, в к-ром все операторы координатдиагональны [т. е. в представлении, где состояние задаётся волновой ф-цией
(здесь выписаны только ненулевые коммутаторы). Вообще, переход от классическогок квантовому описанию физ. системы можно трактовать как замену классических Пуассонаскобок коммутаторами операторов соответствующих величин. Из канонич. <П. с. следует, что каждая пара канонич. переменных qi,pi удовлетворяетсоотношению неопределённостей. В представлении, в к-ром все операторы координатдиагональны [т. е. в представлении, где состояние задаётся волновой ф-цией 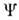 (q1,...,qm),причём
(q1,...,qm),причём 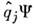 =
=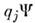 ], операторыимпульсов действуют по правилу
], операторыимпульсов действуют по правилу 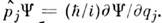 В случае конечного числа степеней свободы все др. корректные представленияканонич. П. с. связаны с описанным посредством нек-рого унитарного преобразования, <т. е. эквивалентны ему. Часто вместо координат и импульсов используют операторырождения
В случае конечного числа степеней свободы все др. корректные представленияканонич. П. с. связаны с описанным посредством нек-рого унитарного преобразования, <т. е. эквивалентны ему. Часто вместо координат и импульсов используют операторырождения 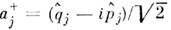 и уничтожения
и уничтожения 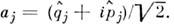
П. с. для них принимают форму
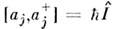 (выписаны только ненулевые коммутаторы). В случае бесконечного числа степенейсвободы (когда т =
(выписаны только ненулевые коммутаторы). В случае бесконечного числа степенейсвободы (когда т =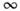 )разл. <представления канонич. П. с. уже не обязательно эквивалентны друг другу. <Обычно используют Фока представление или представление с вакуумом.
)разл. <представления канонич. П. с. уже не обязательно эквивалентны друг другу. <Обычно используют Фока представление или представление с вакуумом.
Важнейшие системы с бесконечным числомстепеней свободы - релятивистские квантовые поля. Так, свободное скалярноебезмассовое веществ. поле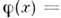
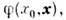 зависящее от времени х 0 и координат х пространств. <точки, задано равенством
зависящее от времени х 0 и координат х пространств. <точки, задано равенством 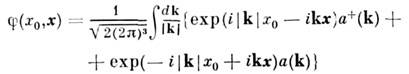
(в системе единиц, в к-рой
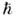 = с=1). Операторные ф-ции a+(k) и a(k) удовлетворяютП. с. [a(k), a+(k')] =
= с=1). Операторные ф-ции a+(k) и a(k) удовлетворяютП. с. [a(k), a+(k')] =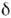 (k- k'), где
(k- k'), где 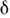 (k)- дельта-функция Дирака. С дискретными операторами рождения и уничтожения a+j и а j функции a+(k) и a(k) связаныравенствами
(k)- дельта-функция Дирака. С дискретными операторами рождения и уничтожения a+j и а j функции a+(k) и a(k) связаныравенствами 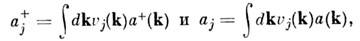
причём {vj(k)}- нек-раяортонормиров. система ф-ций. Свободное поле
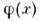 подчинено след. одновременным П. с.:
подчинено след. одновременным П. с.: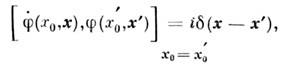
где точка означает производную по времени. <Если времена х 0 и х 0' различны, то
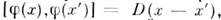 где D(x) - перестановочная функция Паули - Иордана. Взаимодействующиеполя обладают только частью свойств свободных полей, выраженных П. с.,они должны быть локально коммутативны, т. е. их коммутаторы должны обращатьсяв нуль в точках, разделённых пространственноподобным интервалом (см. Локальнаякоммутативность). Одновременные П. с. для взаимодействующих полей теряютсмысл в силу Хаага теоремы.
где D(x) - перестановочная функция Паули - Иордана. Взаимодействующиеполя обладают только частью свойств свободных полей, выраженных П. с.,они должны быть локально коммутативны, т. е. их коммутаторы должны обращатьсяв нуль в точках, разделённых пространственноподобным интервалом (см. Локальнаякоммутативность). Одновременные П. с. для взаимодействующих полей теряютсмысл в силу Хаага теоремы.
Классич. пример П. с. с участием антикоммутаторовили, как говорят, антиперестановочных соотношений - алгебра Дирака матриц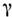 :
: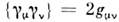 (
(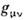 - метрич. тензор,
- метрич. тензор,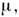
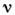 =0,1,2,3; - g00 = gll = g22 = g33=- 1). Физически существенны только эти алгебраич. равенства, конкретныйвыбор
=0,1,2,3; - g00 = gll = g22 = g33=- 1). Физически существенны только эти алгебраич. равенства, конкретныйвыбор 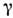 -матрицне играет роли. Антиперестановочным соотношениям удовлетворяет фермионноеспинорное поле
-матрицне играет роли. Антиперестановочным соотношениям удовлетворяет фермионноеспинорное поле 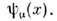 Ненулевые антикоммутаторы для поля
Ненулевые антикоммутаторы для поля 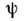 имеют вид
имеют вид 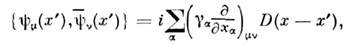
где
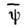 - дираковски сопряжённый к
- дираковски сопряжённый к 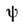 спинор:
спинор: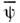 =
=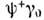 (
(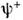 - эрмитово сопряжённый спинор). В релятивистской квантовой теории используютсятакже П. с., в к-рые входят сразу и антикоммутаторы и коммутаторы физ. <величин. Такие П. с. наз. супералгебрами. Если теория инвариантна относительнопреобразований, образующих нек-рую супералгебру, она наз. суперсимметричнойквантовой теорией поля (см. Суперсимметрия).
- эрмитово сопряжённый спинор). В релятивистской квантовой теории используютсятакже П. с., в к-рые входят сразу и антикоммутаторы и коммутаторы физ. <величин. Такие П. с. наз. супералгебрами. Если теория инвариантна относительнопреобразований, образующих нек-рую супералгебру, она наз. суперсимметричнойквантовой теорией поля (см. Суперсимметрия).Лит.: Боголюбов Н. Н., Ширков Д. <В., Введение в теорию квантованных полей, 4 изд., М., 1984; Дирак П. А. <М., Принципы квантовой механики, пер. с англ., 2 изд., М., 1979.
О. И. Завьялов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
