КАНОНИЧЕСКОЕ КВАНТОВАНИЕ

КАНОНИЧЕСКОЕ КВАНТОВАНИЕ

в квантовоймеханике - квантование на основе гамильтонова(иначе - канонич.) формализма, аналогичного гамильтонову формализму классич. механики. <В канонич. формализме осн. переменными являются обобщённые координаты q_k и сопряжённые им (относительно ф-ции Лагранжа Lили ф-ции Гамильтона Н)обобщённые (канонич.) импульсы 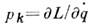Выражая ф-цию Гамильтона консервативной системы с конечным числом степеней свободы N(полную энер гию системы) через канонич. переменные q_k, p_l(k, l=1, 2, . . ., N), ур-ния движения в классич. механике можно записать в виде:

где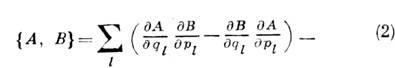

классич. скобка Пуассона, a F(q, p) - динамич. переменная, не зависящая явно от времени (через q, p обозначена совокупность всех q_k, p_l). Поэтому, в частности,

(d_kl- Кронекера символ).
Постулат К. к. состоит в замене переменных q, p на соответствующие операторы., действующие на волновую ф-цию состояния, причём перестановочные соотношения для этих операторов и квантовые ур-ния движения для них получаются из (3) и (4) по "правилу соответствия": классич. скобка Пуассона заменяется на квантовую скобку Пуассона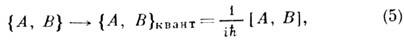

определённую через коммутатор операторов А, В: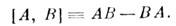

Поэтому ф-лы (3) превращаются в коммутац. соотношения

а квантовые ур-ния движения принимают вид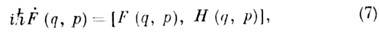

где Н - гамильтониан квантовомеханич. системы. <В квантовой теории поля ф-лы К. к. принимают специфич. форму, отражающую бесконечное число степеней свободы и непрерывный характер переменных, к-рыми характеризуется поле. В качестве обобщённых координат оказывается естественным выбрать значения ф-ции поля j(x, t) в к.-л. произвольный, но фиксированный момент времени t=t₀:

q_k "q(x)=j(c, t₀).

Индекс k, т. о., становится непрерывным и трёхмерным. Канонич. импульс p(x,t₀) удобно определить через лагранжиан поля, точнее через плотность лагранжиана, L:

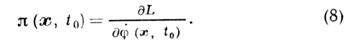
Тогда перестановочные соотношения для обобщённых координат и импульсов поля примут "непрерывный" вид т. н. одновременных перестановочных соотношений: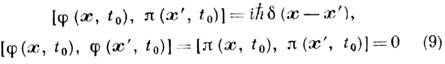

[d (x-x') - трёхмерная ф-ция Дирака], а форма ур-ний движения по сравнению с (7) не изменится. <В квантовой теории релятивистских полей важную роль играют ковариантные перестановочные соотношения вида

где D - нек-рая перестановочная ф-ция ( х, х'- четырёхмерные координаты). Переход от одновременных перестановочных соотношений (9) к разновременным (10) требует решения ур-ний движения для поля j(x) и на практике оказывается возможным лишь для свободных полей. Лит.: Гантлер В., Квантовая теория излучения, пер. с англ., [2 изд.), М., 1956, гл. 2; Вентцель Г., Введение в квантовую теорию волновых полей, пер. с нем., М.-Л., 1947, гл. 1; Боголюбов Н. Н., Ширков Д. В., Квантовые поля, М., изд. 2, 1990, p 6. Д. В. Ширков.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.