ВИНОГРАДОВА ИНТЕГРАЛ — кратный интеграл вида где являющийся средним значением степени 2k модуля тригонометрич. суммы. Теорема Виноградова о величине этого интеграла теорема о среднем лежит в основе оценок сумм Вейля (см. Виноградова метод, Виноградова теорема о… … Математическая энциклопедия
ВИНОГРАДОВА МЕТОД — новый метод оценок три гонометрич. сумм (см. Тригонометрических сумм метод). В. м. позволяет получить очень точные оценки для широкого класса тригонометрич. сумм, в к рых переменная суммирования пробегает значения последовательных целых чисел,… … Математическая энциклопедия
ВИНОГРАДОВА - ГОЛЬДБАХА ТЕОРЕМА — теорема о представлении всех достаточно больших нечетных чисел суммой трех простых. Эта теорема является следствием асимптотич. формулы для числа I(N) решений уравнения в простых числах, доказанной И. М. Виноградовым в 1937: где N нечетное, , См … Математическая энциклопедия
Интеграл Виноградова — кратный интеграл вида где являющийся средним значением степени 2k модуля тригонометрической суммы. Теорема Виноградова о величине этого интеграла теорема о среднем лежит в основе оценок сумм Вейля. Литература Виноградова инте … Википедия
ВИТАЛИ ТЕОРЕМА — 1) В. т. о покрытии. Если система замкнутых множеств является покрытием Витали (см. ниже) множества , то из можно выделить не более чем счетную последовательность попарно непересекающихся множеств , i= 1, 2, 3, . . . , такую, что где т е внешняя… … Математическая энциклопедия
БОРЕЛЯ - ЛЕБЕГА ТЕОРЕМА — о покрытии: пусть А ограниченнее замкнутое множество в Rn и G его открытое покрытие, т;, е: еистема открытых множеств, объединение к рых включает А; тогда существует конечная подсистема множеств , из G(подпокрытие), также являющаяся покрытием А … Математическая энциклопедия
БЭРА ТЕОРЕМА — 1) Б. т. о полных пространствах: любая счетная система открытых и всюду плотных в данном полном метрическом пространстве множеств имеет непустое, п даже всюду плотное в этом пространстве пересечение. Эквивалентная формулировка: полное метрич.… … Математическая энциклопедия
ДЮБУА-РЕЙМОНА ТЕОРЕМА — о единственности разложения функции в ряд: если сумма всюду сходящегося тригонометрич. ряда интегрируема по Риману, то этот ряд является ее рядом Фурье; доказана П. Дюбуа Реймоном [1]. Важный частный случай сходимости тригонометрич. ряда к нулю… … Математическая энциклопедия
ВЕЙЛЯ МЕТОД — в теории чисел метод для получения нетривиальных оценок тригонометрич. сумм вида где а an,...,a1 любые действительные числа. В. м. был разработан Г. Вейлем [1] для установления критериев равномерного распределения (см. Вейля критерий). Сущность В … Математическая энциклопедия
Карацуба, Анатолий Алексеевич — Карацуба Анатолий Алексеевич Дата рождения: 31 января 1937 … Википедия
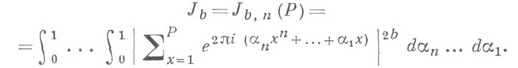
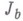- среднее значение тригонометрич. суммы. Формулируется следующим образом. Если при целом неотрицательном tположить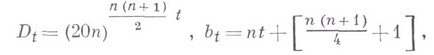 
и целом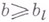 
будет выполняться 
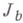, даваемая В. т., предельно точна. В. т. является основной в Виноградова методе оценок Вейля сумм. Кроме того, из нее был получен целый ряд результатов, близких к наилучшим, в классич. проблемах теории чисел (см. Варинга проблема, Гильберта - Камке проблема. Распределение дробных долей многочлена).