- ВИНОГРАДОВА ОЦЕНКИ
название нескольких теорем И. М. Виноградова. Наиболее известными из них являются следующие.
а) В. о. сумм характеров (см. Дирихле характер). Если
- неглавный характер 
, то при 
б) В. о. сумм Вейля (см. Вейля сумма). Пусть n - постоянное число с условием
и пусть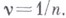 
Пусть далее точки n-мерного пространства разбиты на два класса - точки класса 1 и точки класса 2. Т о ч-кой класса 1 наз. точка
где первые слагаемые - рациональные несократимые дроби с положительными знаменателями, имеющими общим наименьшим кратным число Q, не превосходящее
, а вторые слагаемые удовлетворяют условию
Точкой класса 2 наз. точка, не являющаяся точкой класса 1. Тогда, если положить
то для точек класса 2 при
будет выполняться 
Если же положить
то для точек класса 1 при
будет выполняться
или также
в) В. о. тригонометрических сумм с простыми числами. Пусть
И пусть, в обозначениях теоремы б), точки n-мерного пространства разбиты на классы следующим образом.
К классу 1a отнесены точки, удовлетворяющие условиям
К классу 1b отнесены точки, не являющиеся точками класса 1aи удовлетворяющие условиям
Наконец, к классу 2 отнесены все остальные точки. Если положить для точек класса 1а
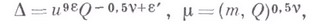
или также
для точек класса 1b, взяв
положить
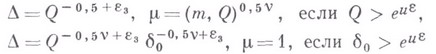
(при
можно брать любую из указанных пар значений 
и 
); и, наконец, для точек класса 2 положить
то при
всегда будет выполняться
Лит.:[1] Виноградов И. М., Метод тригонометрических сумм в теории чисел, М., 1971; [2] Xуа Лo-гeн. Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964. А. А. Карацуба.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
