ВИНОГРАДОВА МЕТОД

- новый метод оценок три-гонометрич. сумм (см. Тригонометрических сумм метод). В. м. позволяет получить очень точные оценки для широкого класса тригонометрич. сумм, в к-рых переменная суммирования пробегает значения последовательных целых чисел, последовательных простых чисел и т. д., что, в свою очередь, дает возможность решить целый ряд классич. проблем аналитич. теории чисел (распределение дробных долей широкого класса функций, распределение простых чисел в натуральном ряде, аддитивные проблемы, частными случаями к-рых являются проблемы Варинга и Гольдбаха, и др.).

Различают две части В. м.: метод оценок Вейля сумм и метод оценок тригонометрич. сумм с простыми числами. Обе части метода используют основную идею И. М. Виноградова - идею сглаживания двойной тригонометрич. суммы, к-рая состоит в следующем. Пусть дана сумма

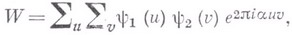
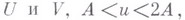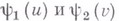где переменные суммирования и п и пробегают значения целых чисел (не обязательно последовательные) в количестве, соответственно, а - произвольные комплекснозначные функции. Тогда

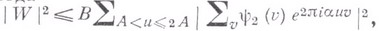
где ипробегает последовательные целые числа интервала (сглаживание),

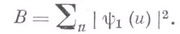
В. м. оценок сумм Вейля. Оцениваются суммы

где причем -действительные числа. При 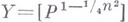будет

где а буквой Wобозначена двойная сумма по хи у, и Далее, обозначив выражение

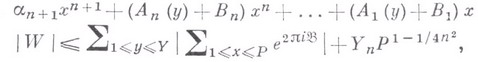
при любых из области

При любом целом :

где 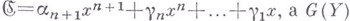- максимальное число совпадений точек с координатами

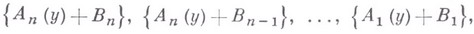
причем фигурные скобки обозначают дробную часть числа, а уменяется в пределах от 1 до Y, и ,

При определенных арифметич. свойствах коэффициентов многочлена f(x).для величины G(Y).можно получить оценку Кроме того, последний интеграл не превосходит числа решений системы уравнений:

Для оценки числа решений этой системы используется Виноградова теорема о среднем, к-рая является основной в В. м. оценок сумм Вейля (см. Виноградова оценки). В. м. оценок тригонометрических сумм спростыми числами. Оцениваются суммы

где 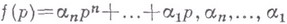- действительные числа. Пусть 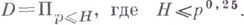С помощью известного свойства функции Мебиуса 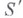сводится к небольшому числу сумм (это число не превосходит 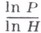) вида

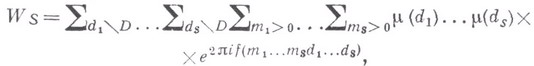
где 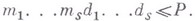В кратной сумме 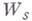переменные пробегают сплошные интервалы суммирования. Те суммы 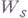, в к-рых интервал суммирования хотя бы по одной переменной тдлинный, оцениваются с помощью В. м. оценок сумм Вейля. В противном случае длинным будет интервал суммирования по одной из переменных суммирования 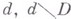. Тогда применяется следующая лемма И. М. Виноградова, к-рая вместе с идеей сглаживания двойных сумм является основной в В. м. оценок тригонометрич. сумм с простыми числами.

Лемма. Пусть 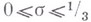и D - произведение всех простых чисел, не превосходящих 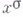, тогда все делители dчисла D, не превосходящие х, можно распределить среди менее чем совокупностей со следующими свойствами:

а) числа d, принадлежащие одной совокупности, обладают одним и тем же числом 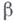простых сомножителей и, следовательно, одним и тем же значением ;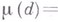

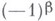б) одна из совокупностей, к-рая наз. простейшей, состоит из одного числа d=1. Для каждой из остальных совокупностей имеется свое такое, что все числа этой совокупности удовлетворяют условию

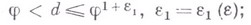
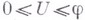в) для всякой совокупности, отличной от простейшей, при любом с условием существуют две совокупности чисел d:числа и 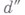с отвечающими им числами и , к-рые удовлетворяют условиям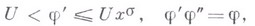

такие, что при нек-ром натуральном Ввсе числа выбранной совокупности, каждое Враз получим, если из всех произведений выберем лишь удовлетворяющие условию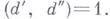

Применяя пункт в) этой леммы с надлежащим значением U, получают

где переменные ии vпробегают длинные интервалы суммирования. Из этой леммы может быть выведена оценка И. М. Виноградова тригонометрич. суммы с простыми числами (см. Виноградова оценки).

Если 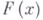в определенном смысле хорошо приближается многочленом, то В. м. позволяет оценивать суммы вида

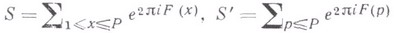
(см. [2], [4]). Кроме того, В. м. позволяет оценивать суммы вида

и т. п. Это дает возможность решать проблемы распределения степенных вычетов, первообразных корней и др. в последовательностях вида , где - фиксированное целое число, а рпринимает значения последовательных простых чисел (см. [3], [5]). О применениях В. м. в аналитич. теории чисел см. [1], [2], [4], [5], [6]. Лит.:[1] Виноградов И. М., Метод тригонометрических сумм в теории чисел, М., 1971; [2] его же, Избранные труды, М., 1952; [3] его же, "Изв. АН СССР, Сер. ма-тем.", т. 30, №. 3, 1966, с. 481-96; [4] Карацуба А. А., "Труды Матем. ин-та АН СССР", 1971, т. 112, с. 241-55; 1973,

т. 122, с. 257-61; [5] Xуа Ло -ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964; [6] Чандрасекхаран К., Арифметические функции, пер. с англ., М., 1974. А. А. Карацуба.