АБЕЛЕВА ФУНКЦИЯ

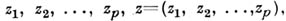- обобщение эллиптической функции одного комплексного переменного на случай многих комплексных переменных. Мероморфная в комплексном пространстве функция f(z) от pкомплексных переменных наз. А. ф., если существуют 2р векторов-строк из С ^p

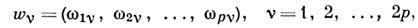
линейно независимых над полем действительных чисел и таких, что 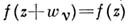для всех 2р. Векторы 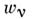наз. периодами, или системами периодов, А. ф. 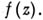Все периоды А. ф. f(z) образуют абелеву группу Г по сложению, наз. группой периодов (или модулем периодов). Базис этой группы наз. базисом периодов А. ф., а также системой основных (или примитивных) периодов. А. ф. наз. 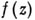вырожденной, если существует такое линейное преобразование переменных к-рое переводит в функцию меньшего числа переменных; в противном случае 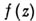наз. невырожденной А. ф. Вырожденные А. ф. характеризуются также тем, что они имеют бесконечно малые периоды, т. е. 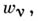для любого числа можно найти период для к-рого

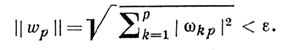
Если 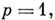то невырожденные А. ф. суть эллиптич. функции одного комплексного переменного. Каждая А. ф. с группой периодов Г естественным образом отождествляется с мероморфной функцией на комплексном торе т. е. на факторпространстве 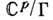(см. также Квазиабелева функция).

Исследование А. ф. началось в 19 в. в связи с проблемой обращения абелевых интеграловI рода (см. Якоби проблема обращения,[1], [2]). Возникающие при решении этой проблемы А. ф. наз. специальными А. ф., а иногда в старых работах под А. ф. только они и подразумевались. Пусть - линейно независимые нормальные абелевы интегралы I рода, построенные на римановой поверхности F:

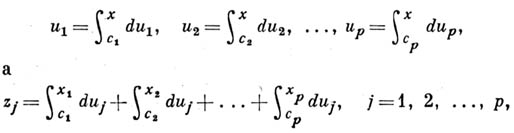
- заданная система сумм, в к-рой нижние пределы интегрирования считаются фиксированными на поверхности F. Тогда специальные А. ф. можно определить как все рациональные функции координат рверхних пределов рассматриваемых в свою очередь как функции от рточек поверхности F. В символической записи, ведущей свое начало от К. Вейерштрасса (К. Weierstrass), любую специальную А. ф. Аl(z) можно изобразить в виде

Соответствующие специальным А. ф. комплексные торы 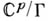являются Якоби многообразиями алгебраич. кривых.

Матрица W, столбцы к-рой образуют базис периодов А. ф. f(z), имеет размер 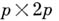и наз. матрицей периодов А. ф. 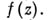Для того чтобы данная матрица Wразмера ~ была матрицей периодов нек-рой невырожденной А. ф. 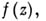необходимо и достаточно, чтобы она удовлетворяла определенным условиям (условия Римана- Фробениуса). Она должна являться римановой матрицей, т. е. для Wдолжна существовать такая антисимметрическая неособенная целочисленная квадратная матрица Мпорядка 2р, что: 1) 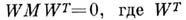- транспонированная матрица W;2) матрица iWMW*^T определяет положительно определенную эрмитову форму (см. [3]). Если выразить условия 1) и 2) в виде соответственно уравнений и неравенств, то получится система р( р -1)/2 римановых уравнений и р( р-1)/2 римановых неравенств. Число рназ. родом матрицы Wи соответствующей А. ф. f(z). Столбцы 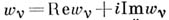матрицы W, рассматриваемые как векторы в действительном евклидовом пространстве R^2p, определяют параллелотоп периодов А. ф.

Все А. ф., соответствующие одной и той же матрице периодов W, образуют абелево функциональное поле K_W. В случае, когда поле К _W содержит невырожденную А. ф., степень его трансцендентности над полем равна р;тор 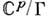при этом является абелевым многообразием, а К _W совпадает с его полем рациональных функций. Если же все А. ф. из 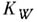вырожденные, то 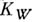изоморфно полю рациональных функций на абелевом многообразии, размерность к-рого меньше р. См. также Квазиабелева функция.

Подобно эллиптич. функциям, каждая А. ф. может быть представлена в виде отношения двух целых трансцендентных тета-функций, представимых в свою очередь в виде тета-рядов. Задание римановой матрицы Wопределяет класс тета-рядов, позволяющий построить все А. ф. поля К _W.

Для специальных А. ф. матрица Wпосредством линейного преобразования независимых переменных , 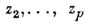всегда может быть приведена к виду

При этом римановы соотношения между элементами матрицы 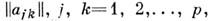должны обеспечивать симметрию этой матрицы, и положительную определенность матрицы действительных частей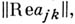

Однако при независимых среди элементов 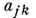матрицы будет только т. е. столько, сколько конформных модулей имеет риманова поверхность F, на к-рой решается проблема обращения (см. Модули римановой поверхности). Помимо римановых соотношений, в этом случае между существует соотношений трансцендентной природы, явный вид которых для случая 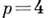впервые нашел в 1886 Ф. Шотки (F. Schottky; обзор последующих достижений по этой проблеме см. в [5]).

Специальные А. ф. представимы в виде отношения двух целых тета-функций с полуцелыми характеристиками специального вида. Из этого представления вытекает ряд свойств специальных А. ф., обобщающих многие свойства эллиптич. функций; так: производные А. ф. по любому аргументу суть А. ф.; любые А. ф. связаны алгебраич. уравнением; любую А. ф. можно выразить рационально через 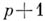нек-рых А. ф., напр, через произвольную А. ф. и ее р частных производных 1-го порядка; для А. ф. справедлива теорема сложения, т. е. значение А. ф. в точке 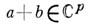можно выразить рационально через значения нек-рых А. ф. в точках

А. ф. имеют большое значение в алгебраич. геометрии как средство униформизации алгебраич. многообразий определенных классов.